Question: Question 1 entire function defined by For nonnegative integer k, the Bessel function of order k is an Je(2) = (-1)zk+2n n!(k + n)!2k+2n

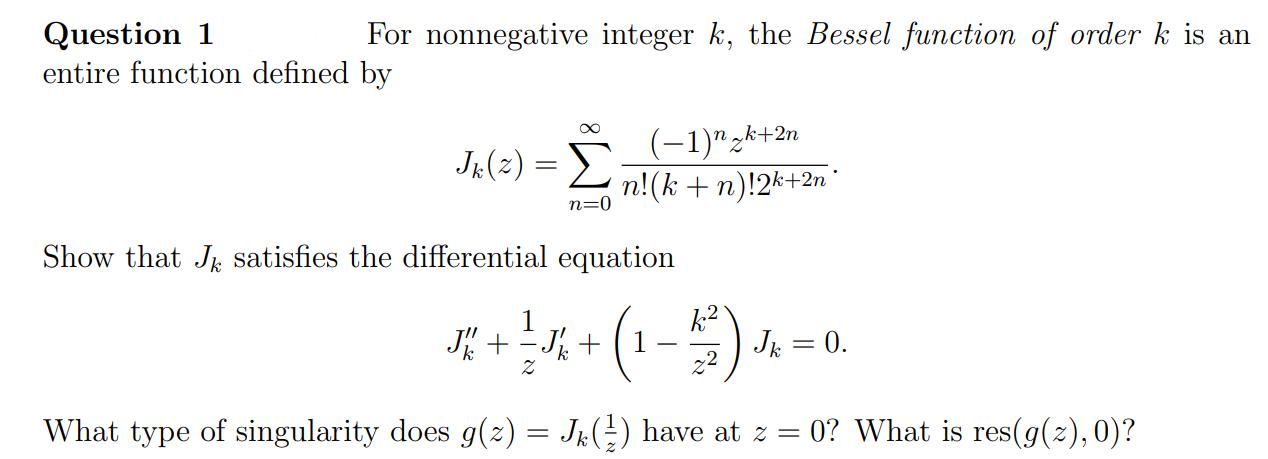
Question 1 entire function defined by For nonnegative integer k, the Bessel

Question 1 entire function defined by For nonnegative integer k, the Bessel function of order k is an Je(2) = (-1)"zk+2n n!(k + n)!2k+2n n=0 Show that J satisfies the differential equation (1-) -. k2 Jk = 0. z2 J" + -J + What type of singularity does g(2) = Jk() have at z = 0? What is res(g(2), 0)?

Step by Step Solution

★★★★★

3.37 Rating (153 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

The Bessel function of order 0, y = J(x), satisfies the differential equation xy" + y' + xy = 0 for all values of and its value at 0 is J(0) = 1. (a) Find J'(0). (b) Use implicit differentiation to...

The function J1 defined by Is called the Bessel function of order 1. (a) Find its domain. (b) Graph the first several partial sums on a common screen. (c) If your CAS has built-in Bessel functions,...

For which nonnegative integers n is 2n + 3 2n? Prove your answer.

26 200 Accounte Recevable 53.800 12,000 Below is the trial balance of Saturn Corporation on December 31, 2019. The accounts are listed in alphabetical order and all accounts have normal balances....

Planning Demand and Supply in a Supply Chain Capacity Planning and Assignment 1 utdallas.edu/~metin Outline Capacity Planning Product-to-plant Assignment utdallas.edu/~metin 2 Deterministic Capacity...

JPMA-01726; No of Pages 12 Available online at www.sciencedirect.com ScienceDirect International Journal of Project Management xx (2015) xxx - xxx www.elsevier.com/locate/ijproman Does Agile work? A...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

The Basics of Financial Mathematics Spring 2003 Richard F. Bass Department of Mathematics University of Connecticut c These notes are 2003 by Richard Bass. They may be used for personal use or class...

In this question you will be asked to reflect on a project you have been involved in or observed, in which a design evolved, or could have evolved, through applying a theory of user behaviour. You...

seventh pages Chapter 3 Curve Sketching How much metal would be required to make a 400-mL soup can? What is the least amount of cardboard needed to build a box that holds 3000 cm3 of cereal? The...

Evaluate the manner in which Diversified Electronics has implemented the investment center concept. What pitfalls did it apparently not anticipate? What, if anything, should be done with regard to...

Identify and describe the most possible generic strategy (ies) followed by your corporation. Mention the evidence you find from the corporate site. Use the industry analysis (Five Forces of Porter...

10 You are working through negotiations with stakeholders of your project and want to find ways to more effectively influence. What are the four steps to effective influence according to Dr. Jay...

Q1) The cross section of member A-B is rectangle with sides 50 mm and 100 mm. 200 N/m 2m 1.5 m 100 mm 50 mm a) Draw the Free body diagram for member A-B b) Find the support (reactive forces at joint...

Describe the steps involved in modifying the default password policy in Oracle?Explain

With servant leadership, leaders strive to serve, making the needs of subordinates a priority over their own needs. According to Johnson (2009), servant leadership is centered on four interrelated...

Lyndon's employer withheld $8,700 in state income taxes from Lyndon's wages in 2021. Lyndon obtained a refund of $1,700 in this year for overpayment of state income taxes for 2020. State income taxes...

What is beacon marketing? What are digital wallets?

Match each equation with its graph. Explain your choices. (a) y = x2 (b) y = x5 (c) y = x8

Graphs of the velocity functions of two particles are shown, where is measured in seconds. When is each particle speeding up? When is it slowing down? Explain. (a) (b) VA 1

Prove that if n is a positive integer, then 7n - 1 is divisible by 6.

When you feel sad, why might it help to look at pictures that reawaken some of your best memories?

When a situation triggers the feeling that Ive been here before, you are experiencing __________ __________.

Ebbinghaus forgetting curve shows that after an initial decline, memory for novel information tends to increase slightly. decrease noticeably. decrease greatly. level out.