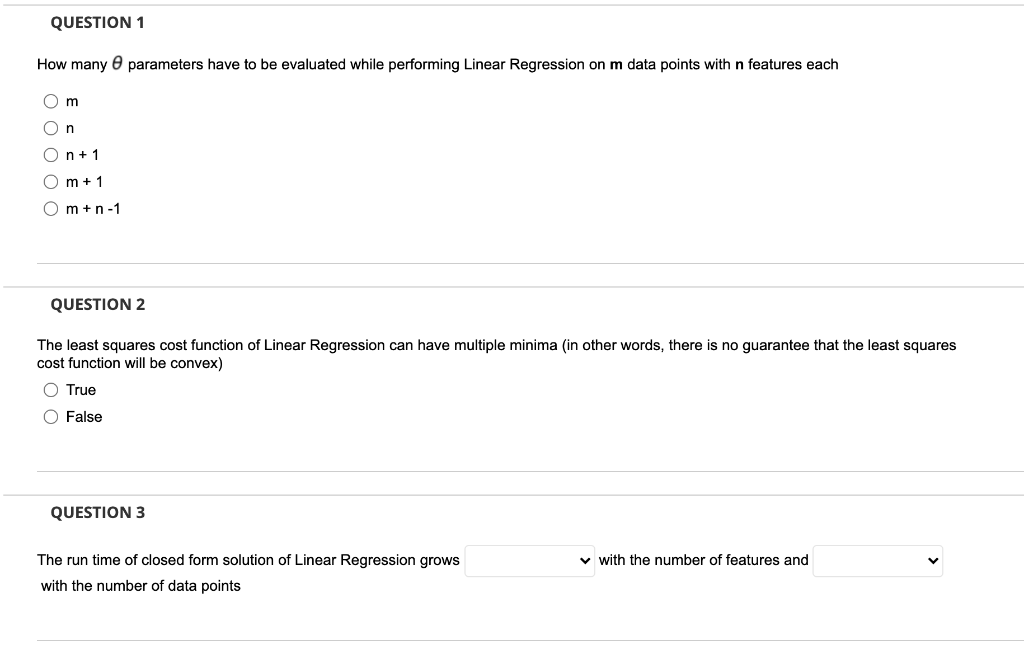
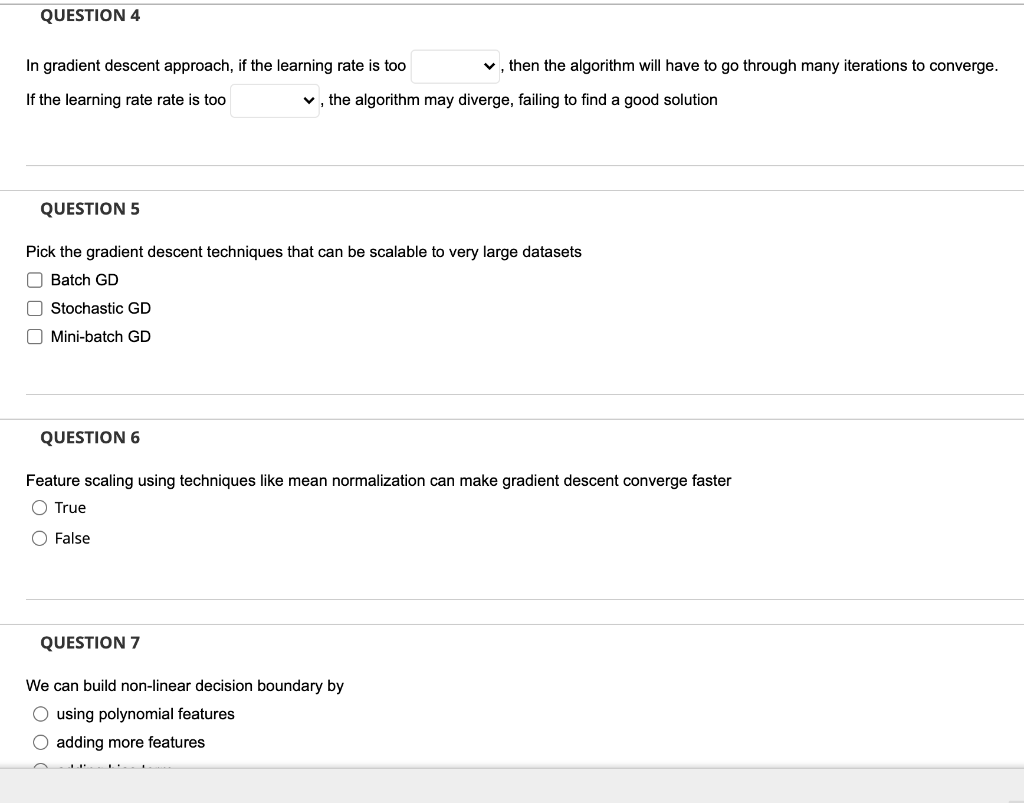
QUESTION 1 How many parameters have to be evaluated while performing Linear Regression on m data points with n features each Om n On + 1 O m + 1 m+ n-1 QUESTION 2 The least squares cost function of Linear Regression can have multiple minima (in other words, there is no guarantee that the least squares cost function will be convex) O True O False QUESTION 3 with the number of features and The run time of closed form solution of Linear Regression grows with the number of data points QUESTION 4 In gradient descent approach, if the learning rate is too , then the algorithm will have to go through many iterations to converge. If the learning rate rate is too , the algorithm may diverge, failing to find a good solution QUESTION 5 Pick the gradient descent techniques that can be scalable to very large datasets O Batch GD Stochastic GD Mini-batch GD QUESTION 6 Feature scaling using techniques like mean normalization can make gradient descent converge faster O True O False QUESTION 7 We can build non-linear decision boundary by O using polynomial features adding more features