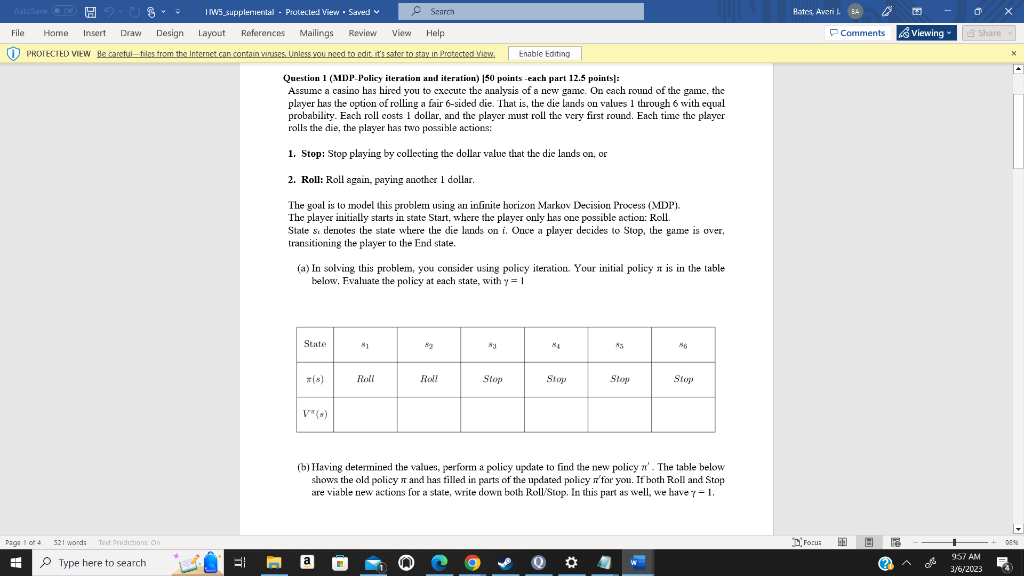
Question: Question 1 (MDP-Policy iteration and iteration) [50 points -each part 12.5 points]: Assume a casino has hired you to execute the analysis of a new
![points]: Assume a casino has hired you to execute the analysis of](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/09/66fa23211c77e_02466fa232096751.jpg)
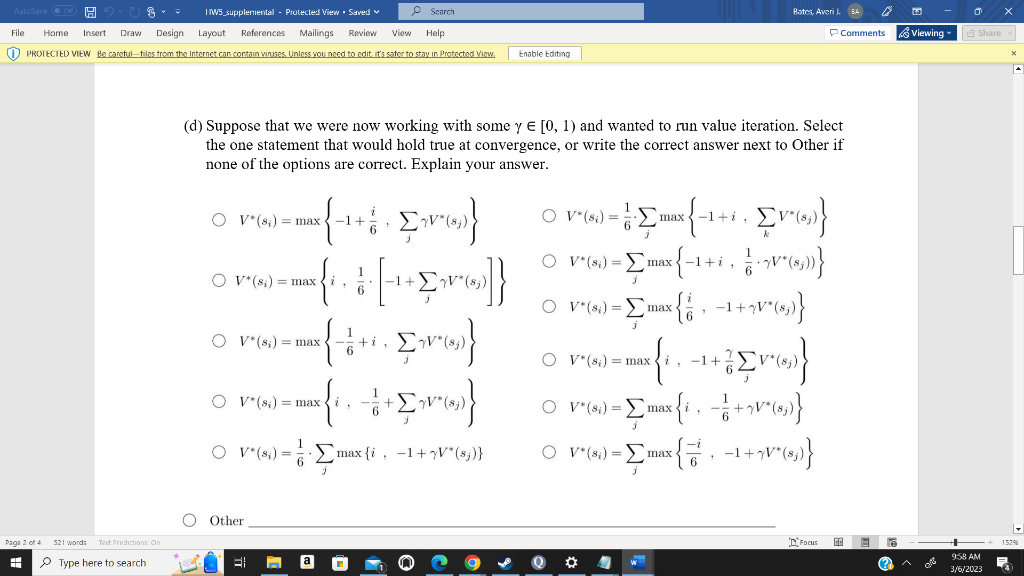
Question 1 (MDP-Policy iteration and iteration) [50 points -each part 12.5 points]: Assume a casino has hired you to execute the analysis of a new gane. On cach round of the game, the player has the option of rolling a fair 6 -sided die. That is, the die lands on values 1 through 6 with equal probability. Each roll costs 1 dollar, and the player must roll the very first round. Each time the player rolls the die, the player has two possible actions: 1. Stop: Stop playing by collecting the dollar value that the die lands on, or 2. Roll: Roll again, paying another 1 dollar. The goal is to model this problern using an infinite horizon Markov Decision Process (MDP). The player initially starts in state Start, where the player only has one possible action: Roll. State si denotes the state where the die lands on i. Once a player decides to Stop, the game is over, transitioning the player to the End state. (a) In solving this problem, you consider using policy iteration. Your initial policy is in the table below. Fvaluate the policy at each state, with y=1 (b) Having determined the values, perform a policy update to find the new policy . The table below shows the old policy and has filled in parts of the updated policy for you. If both Roll and Stop are viable new actions for a state, write down both Roll/Stop. In this part as well, we have =1. (c) Is (s) from part (a) optimal? Explain why or why not. (d) Suppose that we were now working with some [0,1) and wanted to run value iteration. Select the one statement that would hold true at convergence, or write the correct answer next to Other if none of the options are correct. Explain your answer. V(si)=max{1+6i,jV(sj)}V(si)=max{i,61[1+jV(sj)]}V(si)=max{61+i,jV(sj)}V(si)=max{i,61+jV(sj)}V(si)=61jmax{i,1+V(sj)}V(si)=61jmax{1+i,kV(sj)}V(si)=jmax{1+i,61V(sj))}V(si)=jmax{6i,1+V(sj)}V(si)=max{i,1+6jV(sj)}V(si)=jmax{i,61+V(sj)}
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


