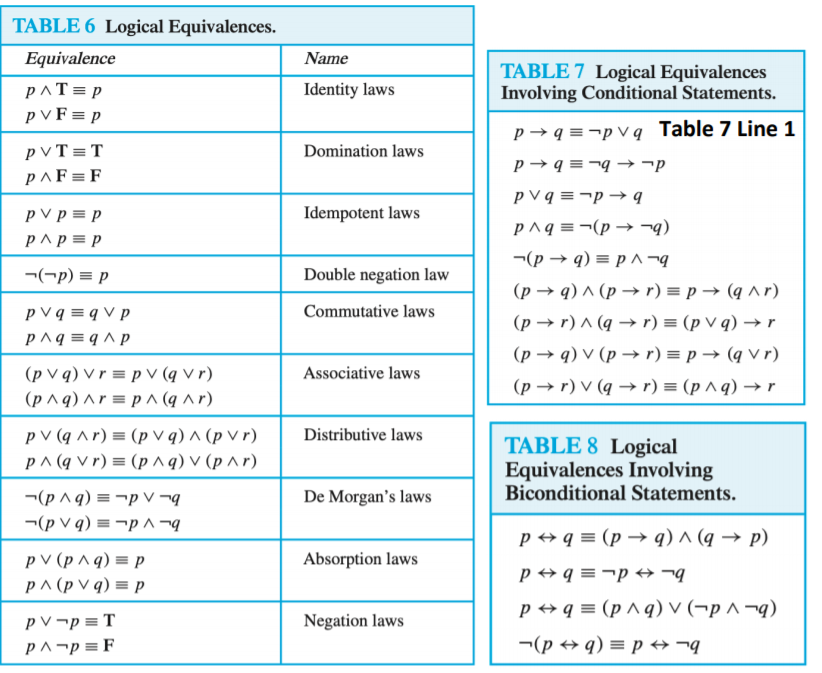
Question 15 (1 point) Problems #15-16-17 go together. Below is a proof that this implication (q(p-q) -p is a Tautology. I have listed all the steps of the proof in the left column. On your scratch paper, list the Logical Equivalence steps for the right column and then choose the correct answer below. I have grouped several answers together, so read them carefully! You may use the provided Tables 6 & 7 of Logical Equivalences from Section 1.3 that I have allowed for Test #1! 1. (q^(p-q) -p 1. Given 2. 3. 2. (9^ (pv-q)) -p 3. ((q^-p) v (94-)) -p 4. ((q4-p) v F) +-p 5. (q^-p) -p 6.-(q^-p) v-p 7. (-qVp) V-p 8. (- vp) v-p 9.-v (pv-p) 10. - VT 11. T 4. 5. 6. 7. 8. 9. 10. 11. 2. Negation; 3. Distributive; 4. Table 7 Line 1 2. Distributive; 3. Table 7 Line 1; 4. Negation 2. Table 7 Line 1; 3. Negation; 4. Distributive None of these 2. Table 7 Line 1; 3. Distributive; 4. Identity 2. Table 7 Line 1; 3. Distributive; 4. Negation Question 16 (1 point) Problems #15-16-17 go together. Below is a proof that this implication (q(p+-q)) -p is a Tautology. I have listed all the Logical Equivalence steps of the proof in the left column. On your scratch paper, list the steps for the right column and then choose the correct answer below. I have grouped several answers together, so read them carefully! You may use the provided Tables 6 & 7 of Logical Equivalences from Section 1.3 that I have allowed for Test #1! 1. (q^(p-9)) -p 1. Given 2. 2. (9^(-pv-)) -P 3.((q^-p) (94-9)) -p 4. ((q4-p) v F)-p 5. (q^-p) -p 6.-(q^-p) v-p 7.( ---) V-p 8. (- vp) v-p 9.-v (pv-p) 10. - VT 11. T 3. 4. 5. 6. 7. 8. 9. 10. 11. 5. Table 7 Line 1; 6. Identity; 7. DeMorgan's 5. Identity; 6. DeMorgan's; 7. Table 7 Line 1 5. Negation; 6. Table 7 Line 1; 7. DeMorgan's 5. DeMorgan's; 6. Table 7 Line 1; 7. Identity None of these 5. Identity; 6. Table 7 Line 1; 7. DeMorgan's TABLE 6 Logical Equivalences. Equivalence PAT=p pvF=p Name Identity laws TABLE 7 Logical Equivalences Involving Conditional Statements. p+q=-pvq Table 7 Line 1 Domination laws pVT=T p AF=F p +9= -9 Idempotent laws pvp = p pp=p -(-p) = p Double negation law Commutative laws pvq=p 9 p1q = -(p -9) -(p 9) = p An (p ) (p + r) = p + (qar) (p +r)^(q + r) = (p Vq) r (p q) v (p + r) = p (qvr) ( pr) v (q + r) = (p19) r pVq=qVP PAq=qp Associative laws (p Vq) vr=pv (vr) (p19) Ar = p ^ (qar) Distributive laws pv (qar) = (pvq) ^ (p vr) PA(q Vr) = (p 9) v (par) TABLE 8 Logical Equivalences Involving Biconditional Statements. De Morgan's laws -(19) =pV-9 -(pvq) = -p4-9 Absorption laws pv (19) = P p^ (p Vq) = p p + q = (p 9) ^ (q + p) p 9 = 9 p #q = (p19) v (219) -(p q) = p + 9 Negation laws pv-p=T PA-p=F