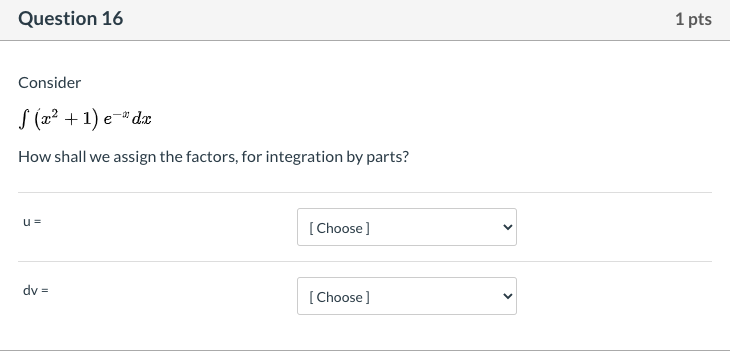
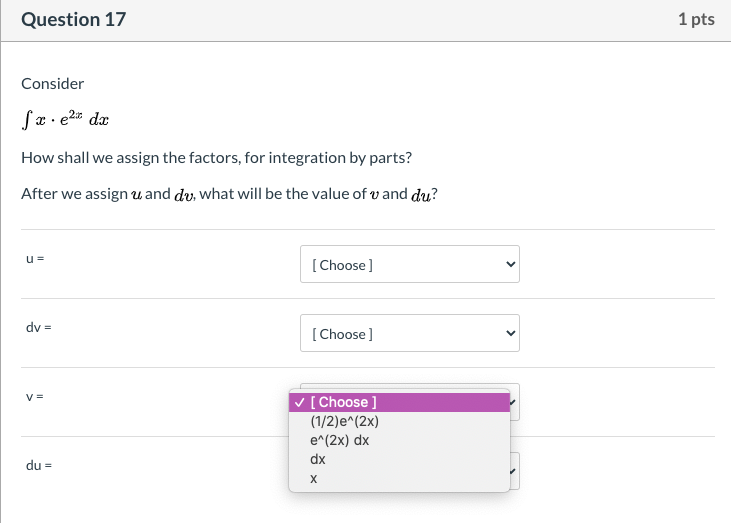
Question: Question 16 1 pts Consider S(' +led How shall we assign the factors, for integration by parts? U = [ Choose ] dv = [
![the factors, for integration by parts? U = [ Choose ] dv](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6704aeefc7e9f_1756704aeefb5a0d.jpg)
![= [ Choose ]Question 16 1 pts Consider How shall we assign](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6704aef023be6_1766704aef009dd5.jpg)
![the factors, for integration by parts? U= [ Choose ] e*(-x) dx](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6704aef084cc8_1766704aef05f10b.jpg)
![(x* 2 + 1) dv = [ Choose ]Question 16 1 pts](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6704aef0e9ca3_1766704aef0cc8d6.jpg)
![parts? U= [ Choose ] v dv = [ Choose ] e*](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6704aef1b4a75_1776704aef19d231.jpg)
![[ Choose ] (1/2)e*(2x) e* (2x) dx dv = dx X V=](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6704aef335627_1796704aef3264f9.jpg)
![[ Choose ] v du = [ Choose ] vQuestion 17 1](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6704aef380fa1_1796704aef370f95.jpg)
![be the value of v and du? U= [ Choose ] v](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6704aef47f707_1806704aef465f6e.jpg)
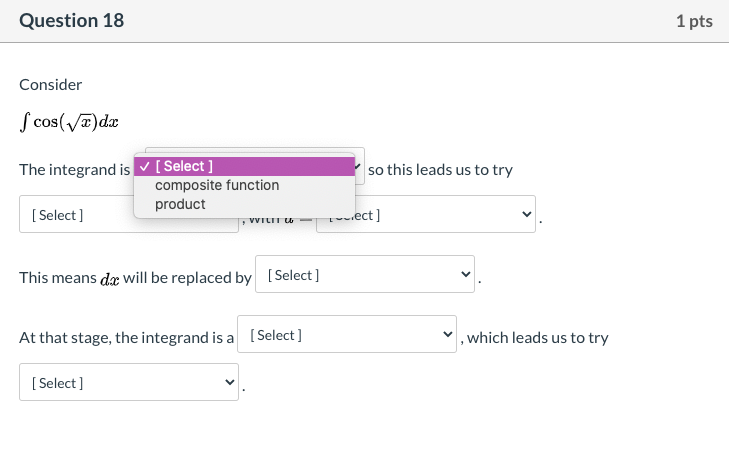
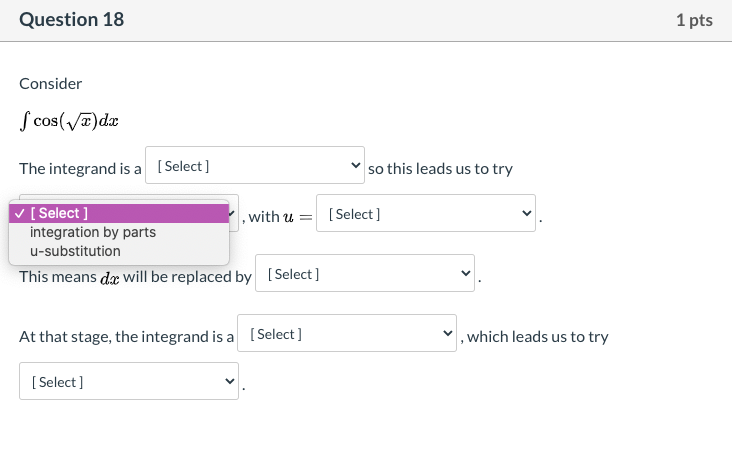
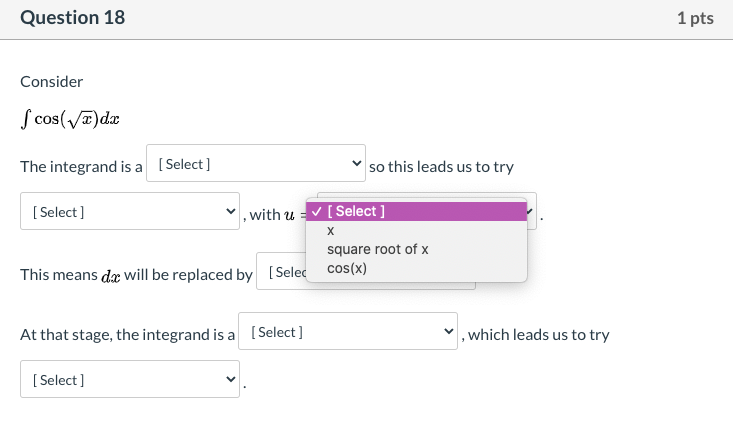
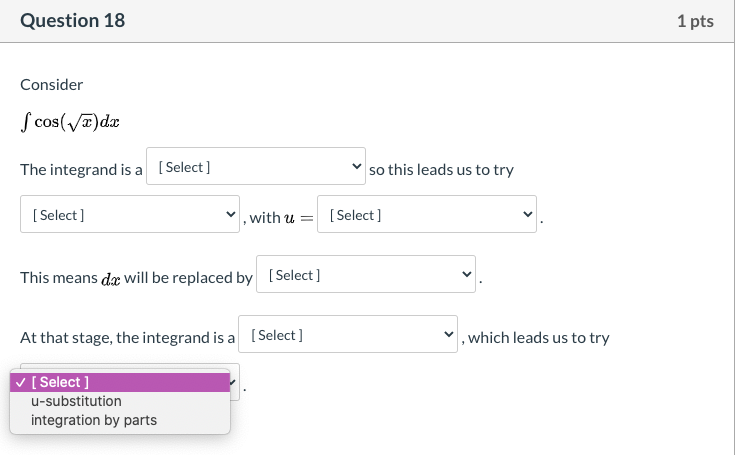
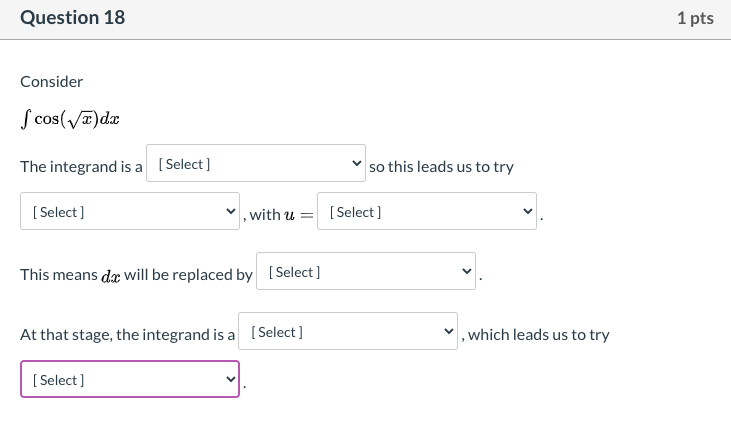
Question 16 1 pts Consider S(' +led How shall we assign the factors, for integration by parts? U = [ Choose ] dv = [ Choose ]Question 16 1 pts Consider How shall we assign the factors, for integration by parts? U= [ Choose ] e*(-x) dx (x* 2 + 1) dv = [ Choose ]Question 16 1 pts Consider f( +leadx How shall we assign the factors, for integration by parts? U= [ Choose ] v dv = [ Choose ] e* (-x) dx (x* 2 + 1)Question 17 1 pts Consider How shall we assign the factors, for integration by parts? After we assign u and do, what will be the value of v and du? U= [ Choose ] (1/2)e*(2x) e* (2x) dx dv = dx X V= [ Choose ] v du = [ Choose ] vQuestion 17 1 pts Consider fa . eat da How shall we assign the factors, for integration by parts? After we assign u and do, what will be the value of v and du? U= [ Choose ] v dv = V [ Choose ] (1/2)e^(2x) e* (2x) dx V= dx X du = [ Choose ]Question 17 1 pts Consider How shall we assign the factors, for integration by parts? After we assign u and do, what will be the value of v and du? U= [ Choose ] V dv = [ Choose ] v V= [ Choose ] (1/2)e*(2x) e* (2x) dx du = dx XQuestion 1? Consider f m - e33 da: How shall we assign the factors. for integration by parts? After we assign it. and d1}, what will be the value Gift! and du? u= ' [Cheese] V' l [ Cheese ] {1I2]E\"i2 Question 18 1 pts Consider S cos( vx)dx The integrand is V [ Select ] composite function so this leads us to try [ Select ] product VVILIT W This means dax will be replaced by [ Select ] At that stage, the integrand is a [ Select ] , which leads us to try [ Select ]Question 18 1 pts Consider f cos( vx) dx The integrand is a [ Select ] so this leads us to try [ Select ] , with u = integration by parts [ Select ] u-substitution This means da will be replaced by [ Select ] At that stage, the integrand is a [ Select ] , which leads us to try [ Select ]Question 18 1 pts Consider f cos(Vx) dx The integrand is a [ Select ] so this leads us to try [ Select ] , with u = v [ Select ] X square root of x This means dax will be replaced by [ Seled cos(x) At that stage, the integrand is a [ Select ] , which leads us to try [ Select ]Question 18 1 pts Consider S cos(vx) da The integrand is a [ Select ] so this leads us to try [ Select ] , with u = [ Select ] This means da will be replaced by [ Select ] du 2*u du At that stage, the integrand is a [ Select ] , which leads us to try [ Select ]Question 18 1 pts Consider S cos(vx) dx The integrand is a [ Select ] so this leads us to try [ Select ] v , with u = [ Select ] This means dax will be replaced by [Select ] At that stage, the integrand is
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


