Question 2\ For integers

k

and

n>0

, show that

cos(2k\\\\pi )/(n)+isin(2k\\\\pi )/(n)

is a primitive

n

th root of unity if and only if

k

and

n

are coprime.\ For an irrational number

\\\\alpha

, show that

cos(2\\\\pi \\\\alpha )+isin(2\\\\pi \\\\alpha )

is not a root of unity.

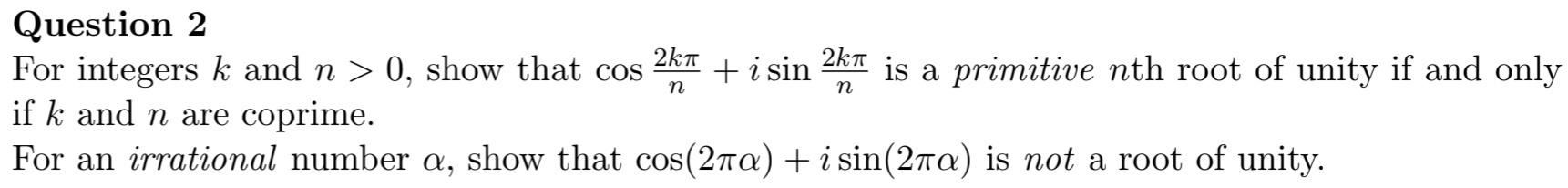
Question 2 For integers k and n>0, show that cosn2k+isinn2k is a primitive nth root of unity if and only if k and n are coprime. For an irrational number , show that cos(2)+isin(2) is not a root of unity