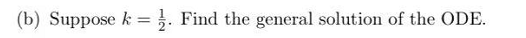
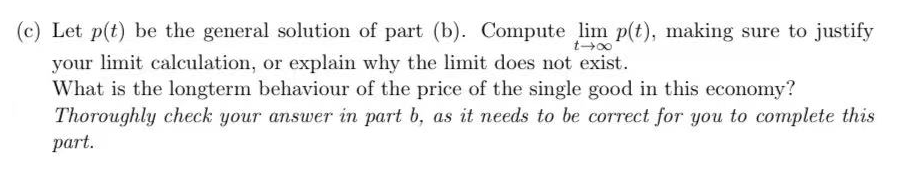
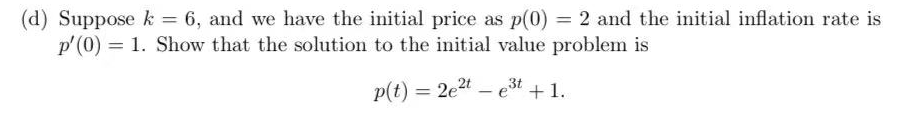
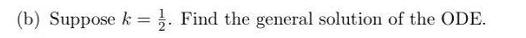
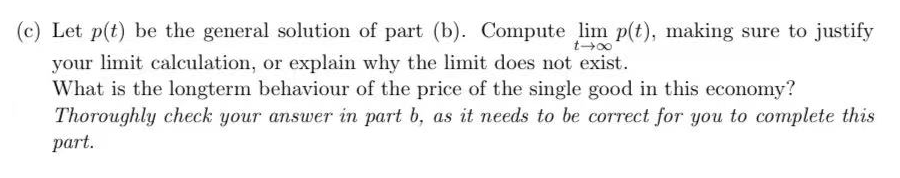
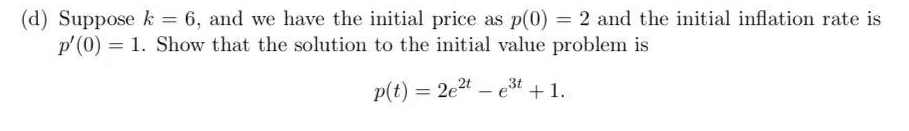
Question 2 In this question, we consider a second order ODE arising from economics that can be used to model how expectations of inflation rates can effect the economy. Consider a simplified model of an economy where there is a single good that is produced with a constant, fixed aggregate supply. Let p(t) be the price of the single good. Then the observed inflation rate is p'(t). An ODE that describes the price p is given by: p"(t) - (k - 1)p'(t) + kp(t) = k. where k > 0 is a constant describing how people's expectations on the rate of inflation changes depending on the observed inflation rate. (a) Show that p(t) = 1 is an equilibrium solution of the ODE. Recall that an equilibrium solution is just a solution that is constant.\f(e) Let 33(t) be the general solution of part (b). Compute lglim pftL making sure to justify Am you: limit calculation, or explain why the limit does not exist. What is the longterm behaviour of the price of the single good in this economy? Thoroughly check your answer in part b, as it needs to be (towed for you to complete this port. (:1) Suppose k = 6, and we have the initial price as 11(0) 2 2 and the initial ination rate is ME!) = 1. Show that the solution to the initial mine problem is p{t) = 24321: 63: +1. More space for 2d) (e) Let p(t) = 2e2t - est + 1 be the solution of the initial value problem from part (d). What happens to p(t) in the long run? (Keep in mind that the price cannot go negative.)