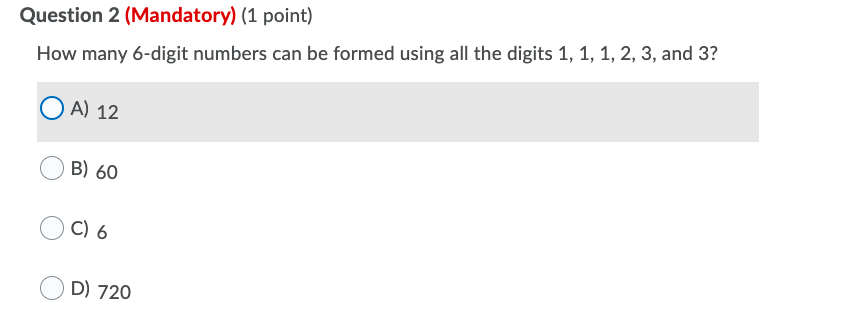
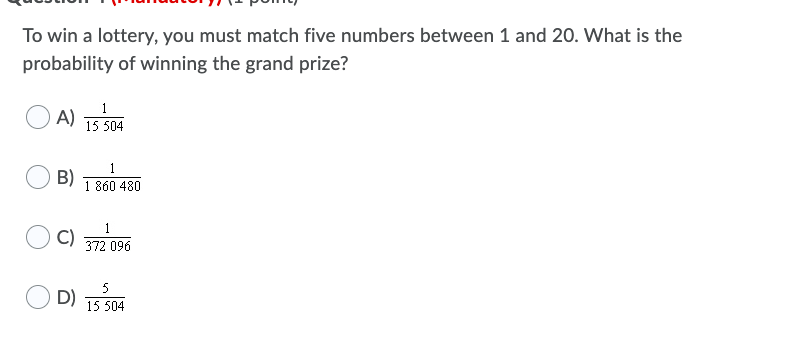
Question 2 (Mandatory) (1 point) How many 6-digit numbers can be formed using all the digits 1, 1, 1, 2, 3, and 3? A) 12 B) 60 C) 6 D) 720 To win a lottery, you must match five numbers between 1 and 20. What is the probability of winning the grand prize? A) B) 15 504 1 860 480 1 372 096 D) 15 504 Which is not a characteristic of a uniform distribution? A) P(x) = 1 B) E(X) n = 22 i-1 C) All outcomes are equally likely in a single trial. D) All trials are dependent and involve success and failure. Which is not a characteristic of a binomial probability distribution? A) E(X) = np B) Trials are dependent. C) Successes are counted on a given number of trials. D) q = 1-p The names of six adults and ten children in a family are written on pieces of paper and put in a hat. Five different slips of paper are drawn from a hat. Identify whether the number of children's names drawn is a binomial or hypergeometric distribution and how to convert it to the other type. A) Hypergeometric; draw the names without replacement. B) Binomial; draw the names with replacement. C) Binomial; draw the names without replacement. D) Hypergeometric; draw the names with replacement. How many arrangements of a string of balloons can be made using three red, four white, and five gold balloons?