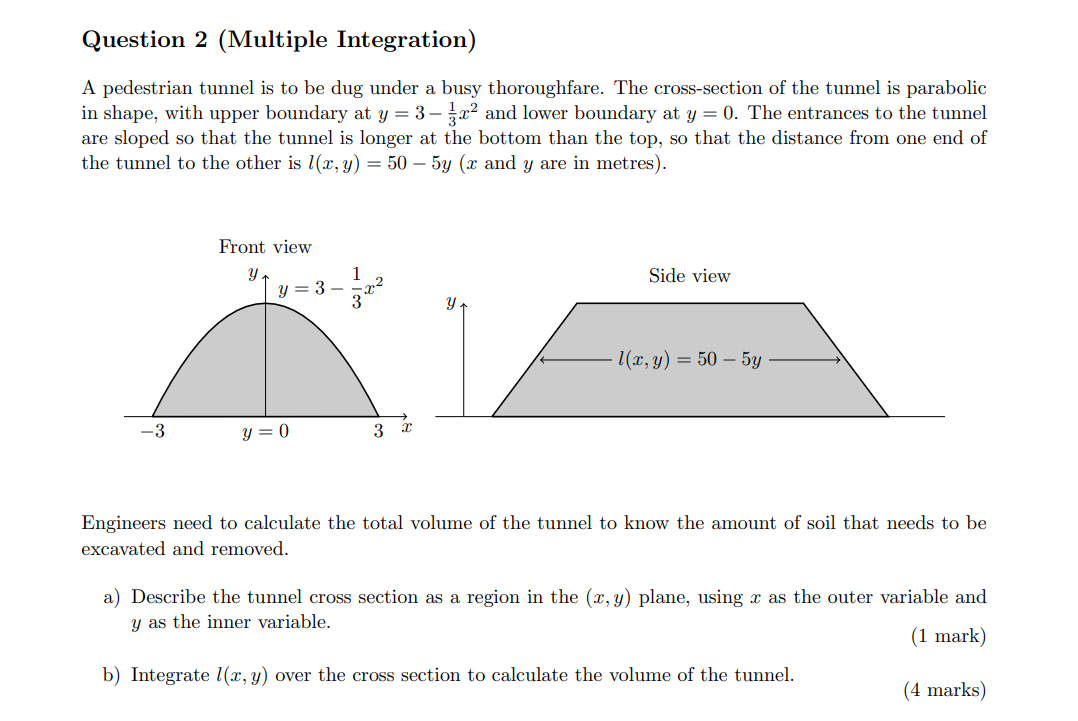
Question 2 (Multiple Integration) A pedestrian tunnel is to be dug under a busy thoroughfare. The cross-section of the tunnel is parabolic in shape, with upper boundary at y = 3 %Tz and lower boundary at y = (. The entrances to the tunnel are sloped so that the tunnel is longer at the bottom than the top, so that the distance from one end of the tunnel to the other is I(x,y) = 50 by (z and y are in metres). Front view Side view Engineers need to calculate the total volume of the tunnel to know the amount of soil that needs to he excavated and removed. a) Describe the tunnel cross section as a region in the (x,y) plane, using x as the outer variable and y as the inner variable. (1 mark) b) Integrate I(x,y) over the cross section to calculate the volume of the tunnel. (4 marks)