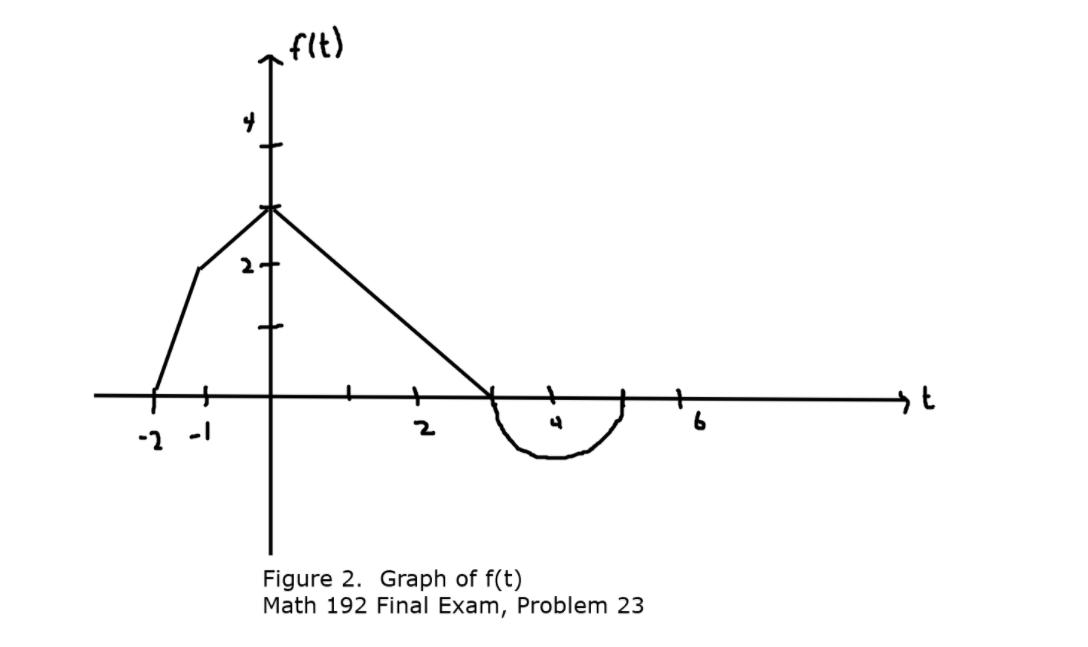
This problem deals with the graph of f(t) given in [Figure 2] We look at the accumulated area beneath this curve, as in the definite integral as follows Fx) = S_ft) f(t) dt { F(x) = int_(-2)^x f(t) dt a) Use ordinary area formulas to compute each of the following: F(-1), F(0), F(3) and F(5) b) Find the value of F(3) - F(0), and sketch the corresponding area on the graph. BONUS(2): Sketch on the graph the area corresponding to F(2+h) - F(2), where h represents some small (positive) quantity. flt) Figure 2. Graph of f(t) Math 192 Final Exam, Problem 23