Question:

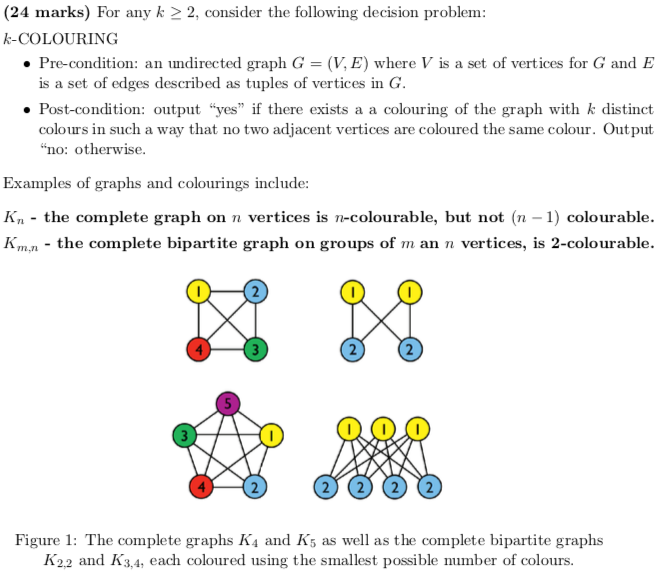
(24 marks) For any k 2 2, consider the following decision problem k-COLOURING Pre-condition: an undirected graph G-(V, E) where V is a set of vertices for G and E is a set of edges described as tuples of vertices in G . Post-condition: output "yes" if there exists a a colouring of the graph with k distinct colours in such a way that no two adjacent vertices are coloured the same colour. Output no: otherwise Examples of graphs and colourings include: Kn the complete graph on n vertices is n-colourable, but not (n-1) colourable. Km n - the complete bipartite graph on groups of m an n vertices, is 2-colourable. 22) 22 Figure 1: The complete graphs K4 and K5 as well as the complete bipartite graphs K2.2 and K3,4, each coloured using the smallest possible number of colours