Question: question 3 (1 point) Let P be the vector space of all polynomials of degree n or less in the variable 3:. Let D :

question 3

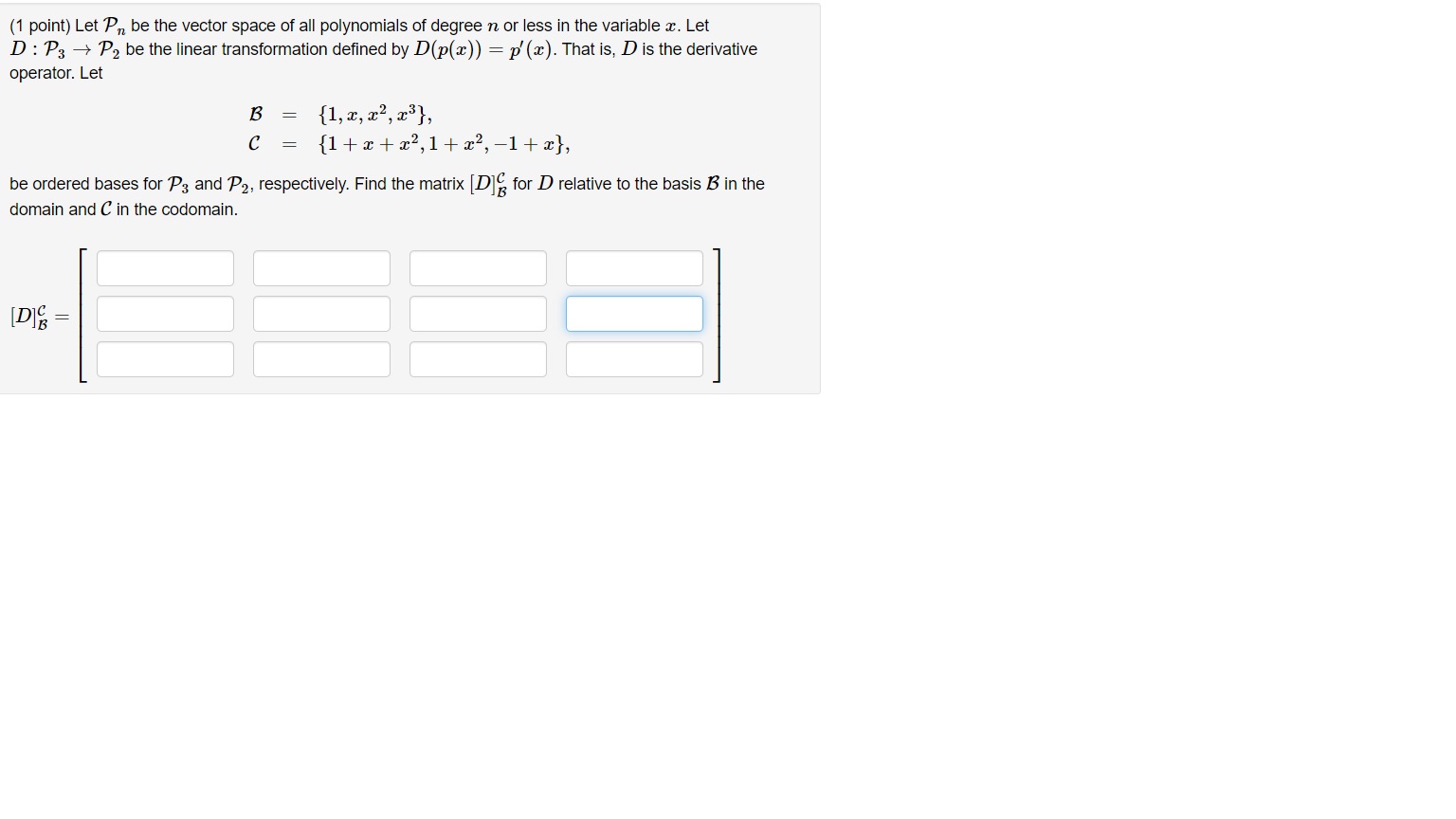
$question 3 (1 point) Let \"P\" be the vector space of all$

(1 point) Let \"P\" be the vector space of all polynomials of degree n or less in the variable 3:. Let D : 'Pa % 7'; be the linear transformation dened by D(p(:1:)) : 1f (2:). That is, D is the derivative operator. Let B = {1,1,12,123}, C 7 {l+z+22,1+12,71+z}, be ordered bases for 133 and P2, respectively. Find the matrix [DE for D relative to the basis B in the domain and C in the oodornain

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

(1 point) Let Pn be the vector space of all polynomials of degree n or less in the variable x. Let D2 : P4 -+ P2 be the linear transformation that takes a polynomial to its second derivative. That...

1 point Let P be the vector space of all polynomials of degree 2 or less and let H be the subspace spanned by 5 5x4 x 2x and x 1 a The dimension of the subspace H is b Is x 5x4 x 2x x 1 a basis for P...

(1 point) Let P, be the vector space of all polynomials of degree 2 or less, and let H be the subspace spanned by 2- (10z + 15z), 7z+ 4z-2 and 1-(5z+7z). a. The dimension of the subspace His b. Is...

Assignment 10: Problem 7 Previous Problem Problem List Next Problem (1 point) Let P2 be the vector space of all polynomials of degree 2 or less, and let H be the subspace spanned by (5x + 4), - (7x2...

(2) (25 pts) Let Vg be the vector space of real polynomials of degree less than or equal to d, and let T : Vi V be the linear map defined by T(P{z)) = P(z+1). Show that 1 is the only eigenvalue of 7....

Let P, be the vector space of all polynomials of degree 2 or less, and let H be the subspace spanned by 6x - 23 - 16, 13x - 3x + 7 and 3x - 12x -8.a. The dimension of the subspace H isb. Is {6x - 23x...

3. Let P;, denote the vector space of all polynomials with degree less than or equal to &. Define a linear transformation T': P; + P; by T(f(x)) = FO) + f'(1)(e-1) + F"(2)(w-2)? + f"(3)(7-3)*. Find...

1. (5 points) Let P3 be the vector space of all polynomials of degree less than 4, with an orthonormal basis (fi, f2, f3, fa}. Let f P3 be such that 1 (,,) = j = 1,2,3,4. Given that f(1) = j, find...

I NEED HELP WITH THIS Let 1P2 be the vector space of all polynomials of degree less than or equal to 2, along with the zero-function. Let H be the subset of 1% given by H={c+t2 | cEIR}. Is H a...

Please give me a detailed solution and answer so that I can compare it with my solving process. 1. Let P denote the vector space of all polynomials and f'(x) denote the derivative of f E P. State...

(a) How is the law of combining volumes explained by Avogadro's hypothesis? (b) Consider a 1.0-L flask containing neon gas and a 1.5-L flask containing xenon gas. Both gases are at the same pressure...

If the checker can only move diagonally, and must jump over X's, how many paths lead to the top? X

( FOB ) : shipping point. How much of the gross profit is treated as foreign source income for purposes of computing the corporation's foreign tax credit in the current year? Multiple Choice \ $ 2 0...

On 1 March 2007 DB Limited issued R560 000 15% debentures at R98. The debentures were to be redeemed at par in four equal annual payments starting 28 February 2010. Required: Journalise the above...