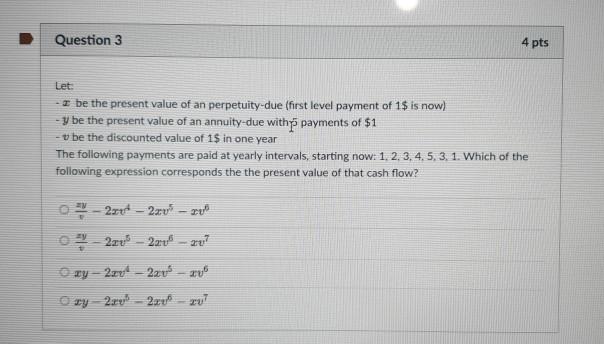
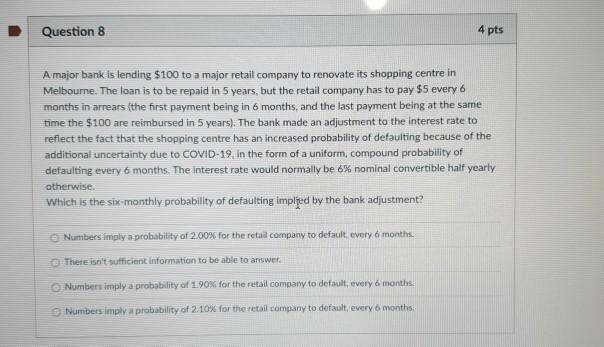
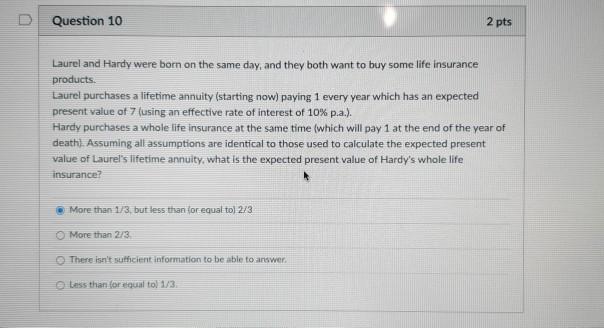
Question 3 4 pts Let: z be the present value of an perpetuity-due (first level payment of 1$ is now) - y be the present value of an annuity-due with payments of $1 - U be the discounted value of 1$ in one year The following payments are paid at yearly intervals, starting now: 1. 2. 3. 4. 5. 3. 1. Which of the following expression corresponds the the present value of that cash flow? - 2001 2xv? - sv" 0-2xv - 2729 2v? ry - 22 - 2x xy2.00 - 2xy! - UT Question 8 4 pts A major bank is lending $100 to a major retail company to renovate its shopping centre in Melbourne. The loan is to be repaid in 5 years, but the retail company has to pay $5 every 6 months in arrears (the first payment being in 6 months, and the last payment being at the same time the $100 are reimbursed in 5 years). The bank made an adjustment to the interest rate to reflect the fact that the shopping centre has an increased probability of defaulting because of the additional uncertainty due to COVID-19. In the form of a uniform, compound probability of defaulting every 6 months. The interest rate would normally be 6% nominal convertible half yearly otherwise Which is the six-monthly probability of defaulting impljed by the bank adjustment? Numbers imply a probability of 2.00% for the retail company to default every 6 months There isn't sufficient information to be able to answer Numbers imply a probability of 1.90% for the retail company to default, every 6 months Numbers imply a probability of 2.10% for the retail company to default, every 6 months Question 10 2 pts Laurel and Hardy were born on the same day, and they both want to buy some life insurance products. Laurel purchases a lifetime annuity (starting now) paying 1 every year which has an expected present value of 7 (using an effective rate of interest of 10% p.a.). Hardy purchases a whole life insurance at the same time (which will pay 1 at the end of the year of death). Assuming all assumptions are identical to those used to calculate the expected present value of Laurel's lifetime annuity, what is the expected present value of Hardy's whole life insurance? More than 1/3. but less than or equal to] 273 More than 2/3 There isn't sufficient information to be able to answer. e less than or equal to 1/3