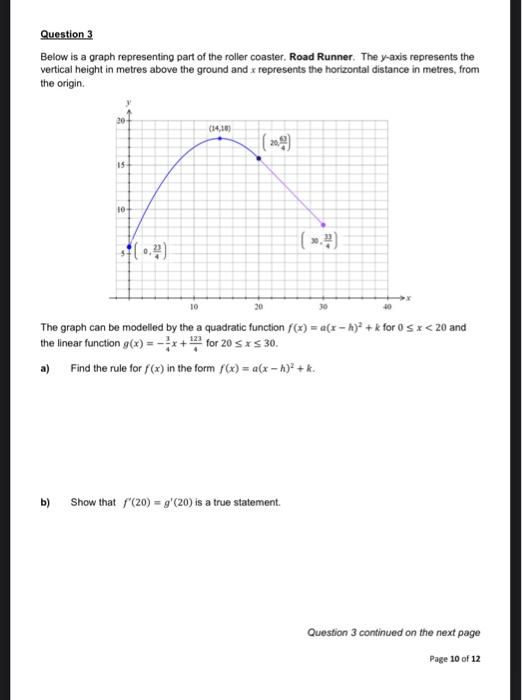
Question 3 Below is a graph representing part of the roller coaster. Road Runner. The y-axis represents the vertical height in metres above the ground and x represents the horizontal distance in metres, from the origin. 20- 15 10+ (14,18) 10 20 The graph can be modelled by the a quadratic function f(x) = a(x-h) + k for 0 x < 20 and the linear function g(x) = x + for 20 x 30. a) Find the rule for f(x) in the form f(x)= a(x-h) + k. b) Show that f'(20) = g'(20) is a true statement. 30 Question 3 continued on the next page Page 10 of 12 Question 3 continues... c) Why would engineers require the gradients of the two functions to be equal at the point of intersection between f(x) and g(x)? Explain. d) e) An additional part h(x) is added to the graph to complete the roller coaster drop. It is created by the following transformation h(x) = -f(x-22) + 24. Find, showing all working, the transformed equation for h(x) if its domain is x (30,36). The equation should be written using full function notation with the rule given in turning point form h(x)= a(x-h) + k. Write a hybrid function, d(x) using all three equations to model the entire cross-section for Road Runner. Page 11 of 12