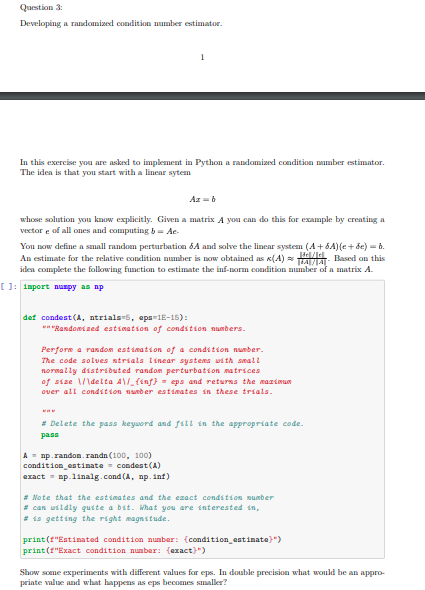
Question 3 Developing a randomized condition number estimator. 1 In this exercise you are asked to implement in Python a randomized condition mmber estimator. The idea is that you start with a linear sytem whose solution you know explicitly. Given a matrix A you can do this for example by creating a vector e of all ones and computing b=A You now define a small random perturbation 8A and solve the linear system (A+8A)(c + de) = 6. An estimate for the relative condition number is now obtained as (A) = /Based on this iden complete the following function to estimate the inf-morm condition number of a matrix A. (): import numpy as np def condest(A, ntrials 5, eps=1E-15): Randomized estimation of condition numbers. Perfore a random estimation of a condition number. The code solves trials linear systems with small normally distributed randon perturbation matrices of size 1/\delta AV_{n} = eps and returns the maximum over alt condition number estimates in these trials. # Delete the pass keyword and fill in the appropriate code. pass A = np.randon randn (100, 100) condition_estinate = condest(A) exact - np. linalg.cond (A, np. int) + Note that the estimates and the exact condition number # can wildly quite a bit. What you are interested in # is getting the right magnitude. print("Estimated condition number: {condition_estinate") print("Exact condition number: (exact)") Show some experiments with different values for eps. In double precision what would be an appro- printe value and what happens as eps becomes smaller? Question 3 Developing a randomized condition number estimator. 1 In this exercise you are asked to implement in Python a randomized condition mmber estimator. The idea is that you start with a linear sytem whose solution you know explicitly. Given a matrix A you can do this for example by creating a vector e of all ones and computing b=A You now define a small random perturbation 8A and solve the linear system (A+8A)(c + de) = 6. An estimate for the relative condition number is now obtained as (A) = /Based on this iden complete the following function to estimate the inf-morm condition number of a matrix A. (): import numpy as np def condest(A, ntrials 5, eps=1E-15): Randomized estimation of condition numbers. Perfore a random estimation of a condition number. The code solves trials linear systems with small normally distributed randon perturbation matrices of size 1/\delta AV_{n} = eps and returns the maximum over alt condition number estimates in these trials. # Delete the pass keyword and fill in the appropriate code. pass A = np.randon randn (100, 100) condition_estinate = condest(A) exact - np. linalg.cond (A, np. int) + Note that the estimates and the exact condition number # can wildly quite a bit. What you are interested in # is getting the right magnitude. print("Estimated condition number: {condition_estinate") print("Exact condition number: (exact)") Show some experiments with different values for eps. In double precision what would be an appro- printe value and what happens as eps becomes smaller
