Question 3 Let's consider the below geometrical layout. 1- Demonstrate that in arbitrary point " ( mathrm{M}^{ ext {", }} ), the radius ( (mathrm{r}) ) has the expression: ( r= ) ( rac{2 F}{1+cos arphi} ) 2- Find the expression of ( F=gleft( heta_{m} ight) ). 3- If ( arphi_{r}=80^{circ} ), Then determine, ( mathrm{r} ) and ( W_{a} @ ) this rim angle and ( mathrm{F}=2.53[mathrm{~m}] ). 4- Determine the concentration ratio ( mathrm{C} ).

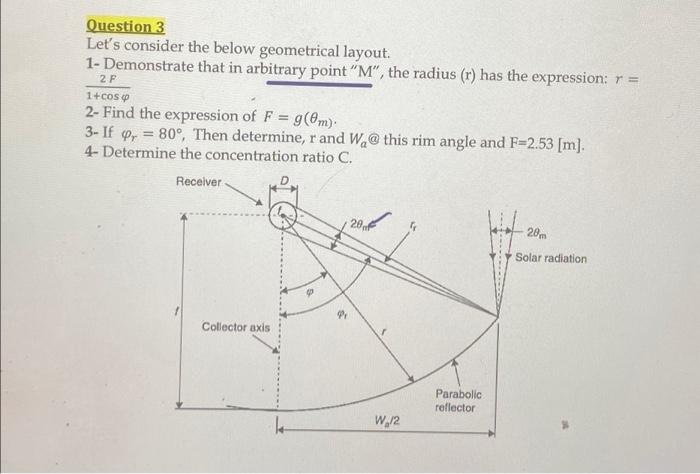
Question 3 Let's consider the below geometrical layout. 1- Demonstrate that in arbitrary point " M ", the radius (r) has the expression: r= 1+cos2F 2- Find the expression of F=g(m). 3- If r=80, Then determine, r and Wa@ this rim angle and F=2.53[m]. 4-Determine the concentration ratio C