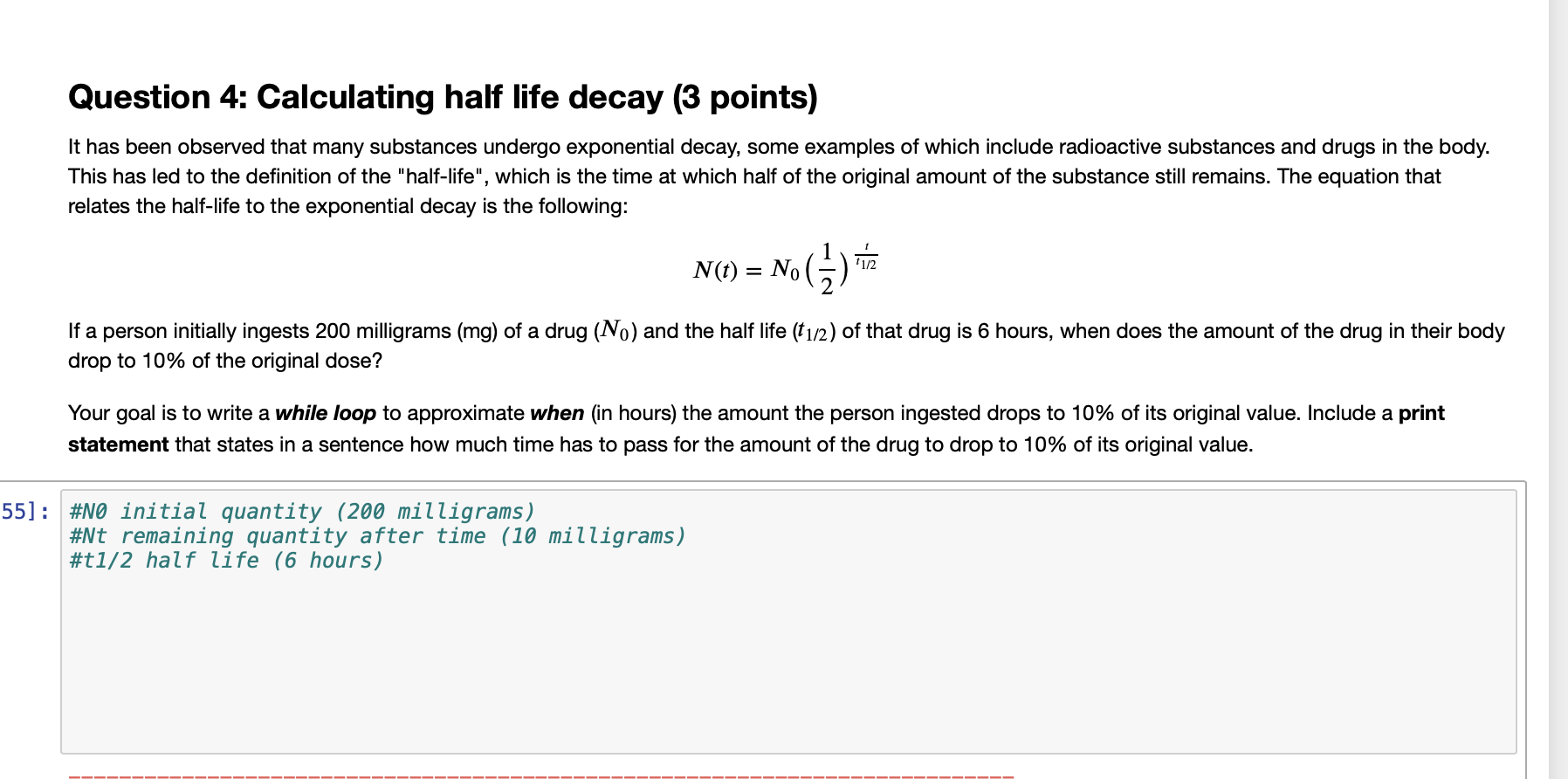
Question 4: Calculating half life decay (3 points) It has been observed that many substances undergo exponential decay, some examples of which include radioactive substances and drugs in the body. This has led to the definition of the "half-life", which is the time at which half of the original amount of the substance still remains. The equation that relates the half-life to the exponential decay is the following: N(t) = No (5) If a person initially ingests 200 milligrams (mg) of a drug (N.) and the half life (t1/2) of that drug is 6 hours, when does the amount of the drug in their body drop to 10% of the original dose? Your goal is to write a while loop to approximate when in hours) the amount the person ingested drops to 10% of its original value. Include a print statement that states in a sentence how much time has to pass for the amount of the drug to drop to 10% of its original value. 551 : #NO initial quantity (200 milligrams) t remaining quantity after time (10 milliarams) #t1/2 half life (6 hours) Question 4: Calculating half life decay (3 points) It has been observed that many substances undergo exponential decay, some examples of which include radioactive substances and drugs in the body. This has led to the definition of the "half-life", which is the time at which half of the original amount of the substance still remains. The equation that relates the half-life to the exponential decay is the following: N(t) = No (5) If a person initially ingests 200 milligrams (mg) of a drug (N.) and the half life (t1/2) of that drug is 6 hours, when does the amount of the drug in their body drop to 10% of the original dose? Your goal is to write a while loop to approximate when in hours) the amount the person ingested drops to 10% of its original value. Include a print statement that states in a sentence how much time has to pass for the amount of the drug to drop to 10% of its original value. 551 : #NO initial quantity (200 milligrams) t remaining quantity after time (10 milliarams) #t1/2 half life (6 hours)