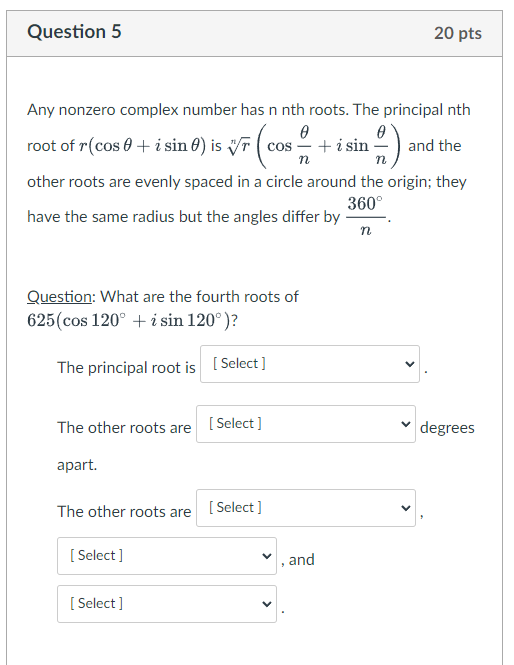
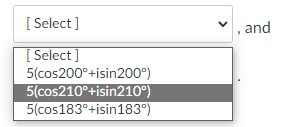
Question: Question 5 20 pts Any nonzero complex number has n nth roots. The principal nth root of r(cos 0 + isin 0) is vr (
![principal root is [ Select ] The other roots are [ Select](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6667d48c5b088_6526667d48c41892.jpg)
![] degrees apart. The other roots are [ Select ] [ Select](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6667d48ca0d7f_6526667d48c91c1e.jpg)
![] , and [ Select ]The principal root is [ Select ]](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6667d48cf3453_6526667d48cd73e7.jpg)
![[ Select ] 156(cos3'+isin3") The other roots are 5(cos30+isin30") degrees 156(cos30*+isin309) apart.](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6667d48d4614f_6536667d48d30ad3.jpg)
![5(cos3+isin3")The other roots are [ Select ] [ Sele st apart. 90](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6667d48d94c7a_6536667d48d7865e.jpg)
![60 The other roots are 120The other roots are [ Select ]](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6667d48dccfab_6536667d48dbd0ca.jpg)
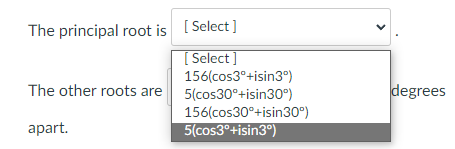
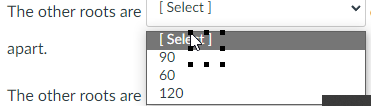
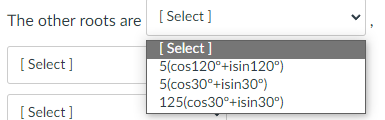
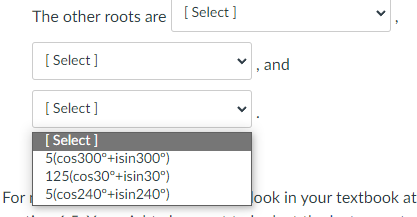
Question 5 20 pts Any nonzero complex number has n nth roots. The principal nth root of r(cos 0 + isin 0) is vr ( cos - + isin and the n n other roots are evenly spaced in a circle around the origin; they 360 have the same radius but the angles differ by n Question: What are the fourth roots of 625(cos 120" + i sin 120" )? The principal root is [ Select ] The other roots are [ Select ] degrees apart. The other roots are [ Select ] [ Select ] , and [ Select ]The principal root is [ Select ] [ Select ] 156(cos3'+isin3") The other roots are 5(cos30+isin30") degrees 156(cos30*+isin309) apart. 5(cos3+isin3")The other roots are [ Select ] [ Sele st apart. 90 60 The other roots are 120The other roots are [ Select ] [ Select ] [ Select ] 5(cos120'+isin120") 5(cos30 +isin30") 125(cos30*+isin30") [ Select ]\fThe other roots are [ Select ] [ Select ] and [ Select ] [ Select ] 5(cos300*+isin300) 125(cos30*+isin309) For 5(cos240*+isin240") ook in your textbook at
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


