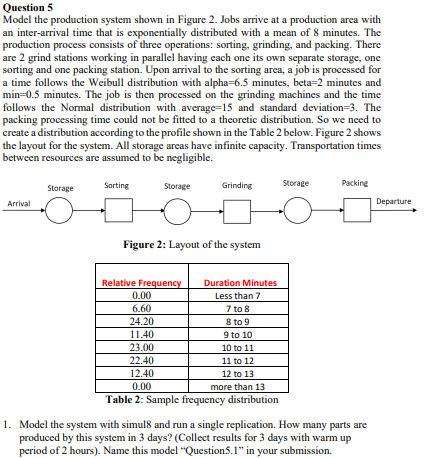
Question 5 Model the production system shown in Figure 2. Jobs arrive at a production area with an inter-arrival time that is exponentially distributed with a mean of 8 minutes. The production process consists of three operations: sorting, grinding, and packing. There are 2 grind stations working in parallel having each one its own separate storage, one sorting and one packing station. Upon arrival to the sorting area, a job is processed for a time follows the Weibull distribution with alpha =6.5 minutes, beta =2 minutes and min =0.5 minutes. The job is then processed on the grinding machines and the time follows the Normal distribution with average =15 and standard deviation =3. The packing processing time could not be fitted to a theoretic distribution. So we need to create a distribution according to the profile shown in the Table 2 below. Figure 2 shows the layout for the system. All storage areas have infinite capacity. Transportation times between resources are assumed to be negligible. Figure 2: Layout of the system Table 2: Sample frequency distribution 1. Model the system with simul8 and run a single replication. How many parts are produced by this system in 3 days? (Collect results for 3 days with warm up period of 2 hours). Name this model "Question 5.1 " in your submission. 2. Assume then that you have the following data: a) Grind 1 has a scheduled maintenance exactly every 6 hours. During this operation that lasts exactly for 20 minutes the station stops working. b) Grind 2 can get random failures for which: a. MTTF follows the Erlang distribution with average 10 and K is 3 . In this we count only the time that the machine has been busy. b. MTTR follows the Exponential distribution with a of 12 . c) The Packing station may sometimes fail in correctly processing the parts. It is recorded that: a. 90% of the parts that leave the packing station were processed correctly and they can leave the system as completed work b. 3% of the parts that leave the packing station are damaged and they have to be scrapped. c. 5% of the parts that leave the packing station are damaged and they should be re-packing. d. 2% of the parts that leave the packing station are substandard grinded parts that need regrinding. So they need to be routed to the Grind 1 station and be treated with higher priority than those from the Grind 1 Queue. In your results summary add the following: - Working\% of both the Grind stations - Failure % of both the Grind stations - Number of parts that left the system as completed worked - Number of parts that were sent to the scrap bin - Number of parts that were re-packed - Number of parts that were re-grinded Run a trial of 50 replications with results collection period 2 days and warm up period 3 hours. Name this model "Question 5.2 " in your submission