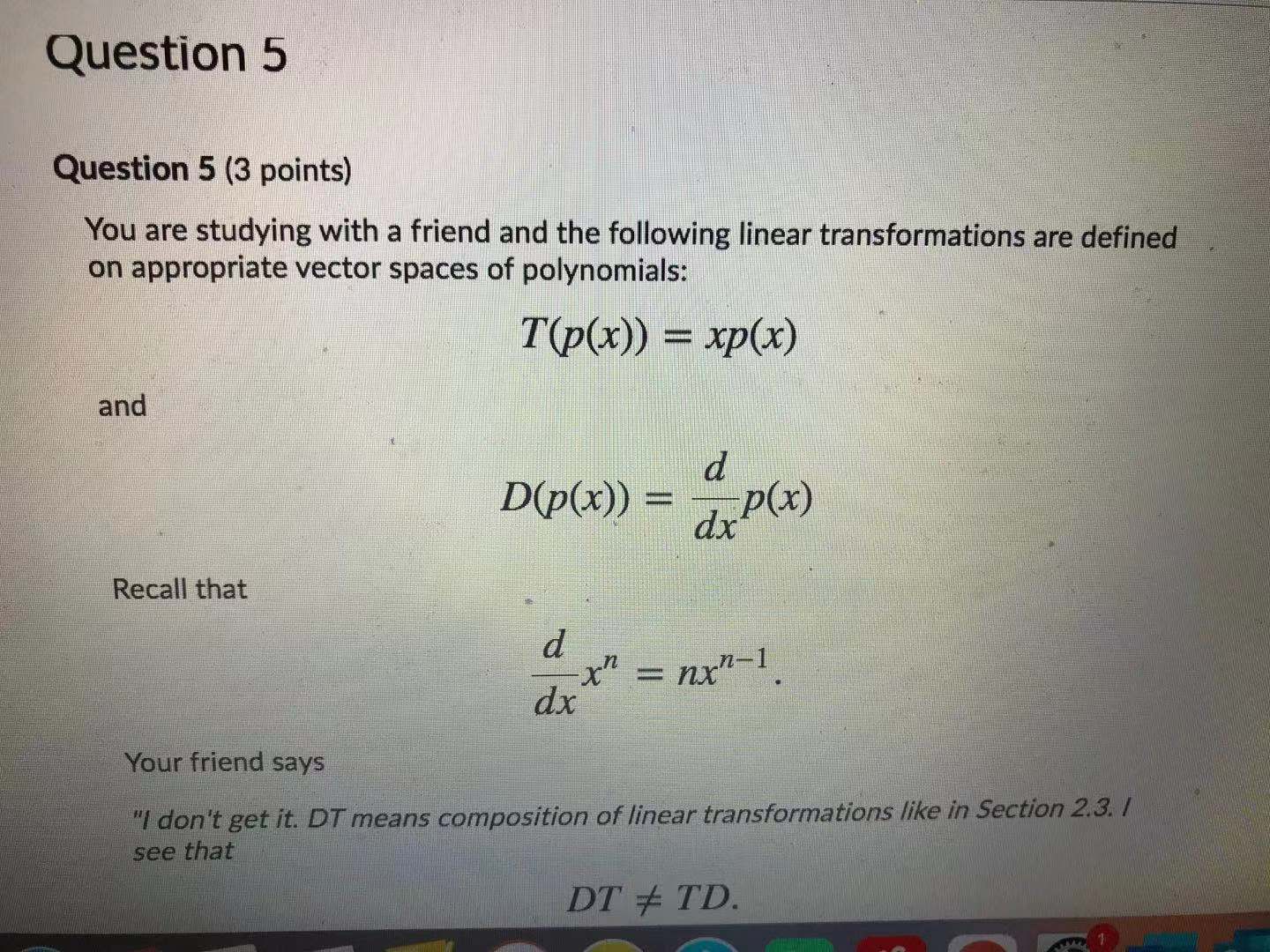
Question 5 Question 5 (3 points) You are studying with a friend and the following linear transformations are defined on appropriate vector spaces of polynomials: T(p(x)) = xp(x) and d D(p(x)) = dx P(x) Recall that d x" = nx7-1. dx Your friend says "I don't get it. DT means composition of linear transformations like in Section 2.3. / see that DT # TD.- Im dx Your friend says "I don't get it. DT means composition of linear transformations like in Section 2.3. / see that DT + TD. But I thought VS1 said vector spaces commute. Why doesn't VS1 apply?" Using 91 (x) =5+3x+2x2 as a counterexample, show your friend is right, DT(q1 (x)) # TD(qi (x)), and then explain in a few sentences why your friend's thinking is wrong for the rest of their statement. I have written out my solution to this problem and will include it in my single PDF file to upload to Gradescope at the end of the test