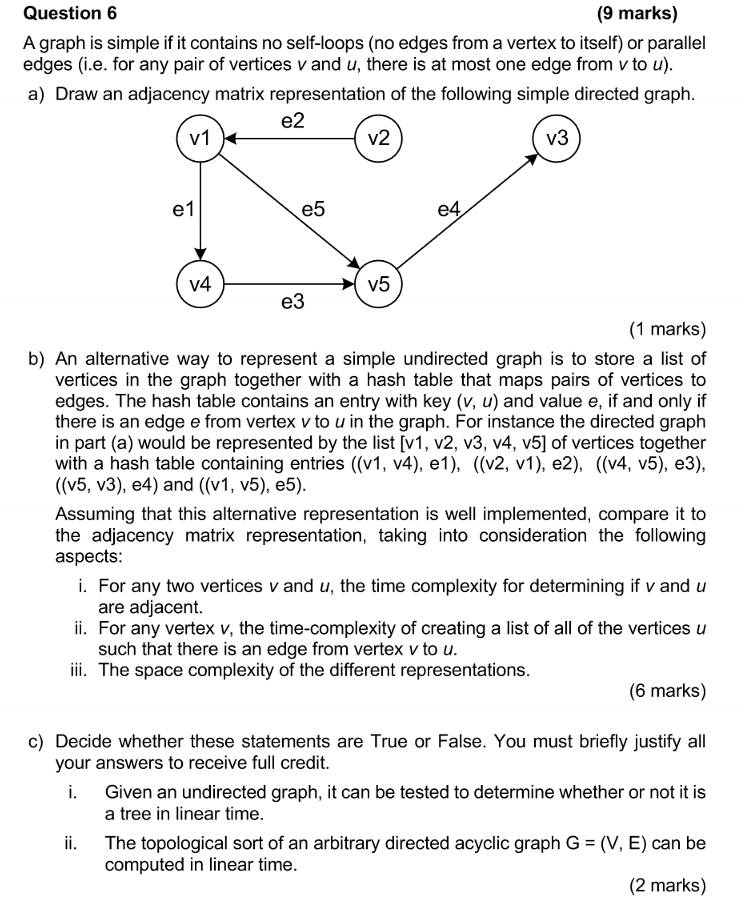
Question 6 (9 marks) A graph is simple if it contains no self-loops (no edges from a vertex to itself) or parallel edges (i.e. for any pair of vertices v and u, there is at most one edge from v to u). a) Draw an adjacency matrix representation of the following simple directed graph. e2 v1 v2 v3 e 1 e5 e4 14 v5 e3 (1 marks) b) An alternative way to represent a simple undirected graph is to store a list of vertices in the graph together with a hash table that maps pairs of vertices to edges. The hash table contains an entry with key (v, u) and value e, if and only if there is an edge e from vertex v to u in the graph. For instance the directed graph in part (a) would be represented by the list [V1, V2, V3, v4, v5] of vertices together with a hash table containing entries ((v1, v4), e1), ((v2, v1), e2), ((v4, v5), e3), ((v5, v3), e4) and ((v1, v5), e5). Assuming that this alternative representation is well implemented, compare it to the adjacency matrix representation, taking into consideration the following aspects: i. For any two vertices v and u, the time complexity for determining if v and u are adjacent. ii. For any vertex v, the time-complexity of creating a list of all of the vertices u such that there is an edge from vertex v to u. iii. The space complexity of the different representations. (6 marks) c) Decide whether these statements are True or False. You must briefly justify all your answers to receive full credit. i. Given an undirected graph, it can be tested to determine whether or not it is a tree in linear time. ii. The topological sort of an arbitrary directed acyclic graph G = (V, E) can be computed in linear time. (2 marks)