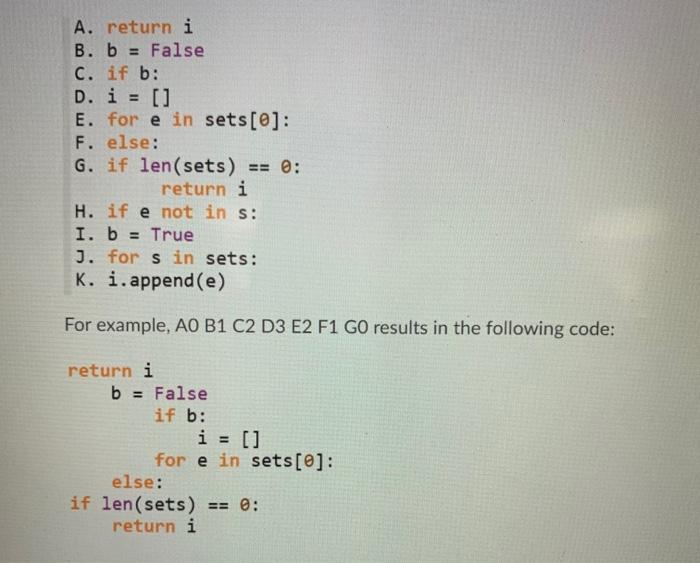
Question 7 (1 point) Consider the following docstring for a function that takes a two-dimensional list of integers as input and returns a list representing the intersection of all the sublists of the input. Note that, as always, the docstring contains only one example, but you are encouraged to think about all possible scenarios. You can safely assume that the sublists of the input list contain only unique elements (i.e. the elements aren't repeated). No other assumption should be made about the input. def get_intersection(sets): *** (list) -> list Returns a list representing the intersection of all the sublists of sets (i.e. the elements the lists have in common with no repetitions) >>> get_intersection([[1, 3, 6], [1, 2, 3, 5, 6], [1, 2, 3]]) [1, 3] The body of the function is made up by the following pieces of code, but they have been shuffled around. Please write the letters in the correct order to recompose the body of the function. After each letter, write a number corresponding to the number of tabs (indentation level) that code should have. E.g., AO means to keep the A code block at the margin (no extra indentation): A1 means to indent all the code in A by one tab, and so on. Please note that each letter should be used at most once. A. return i B. b = False c. if b: D. i = [] E. for e in sets[@]: F. else: G. if len(sets) == 0: return i H. if e not in s: I. b = True J. for in sets: K. i.append(e) For example, AO B1 C2 D3 E2 F1 GO results in the following code: return i b = False if b: i = [] for e in sets[@]: else: if len(sets) == 0: return