Question: Question 8 Question 8 Gasoline Blending Model Gasoline Inputs Octane Rating Regular Supreme Used Available Cost Input 1 150 0 150.0 150 $17.25 100 The
Question 8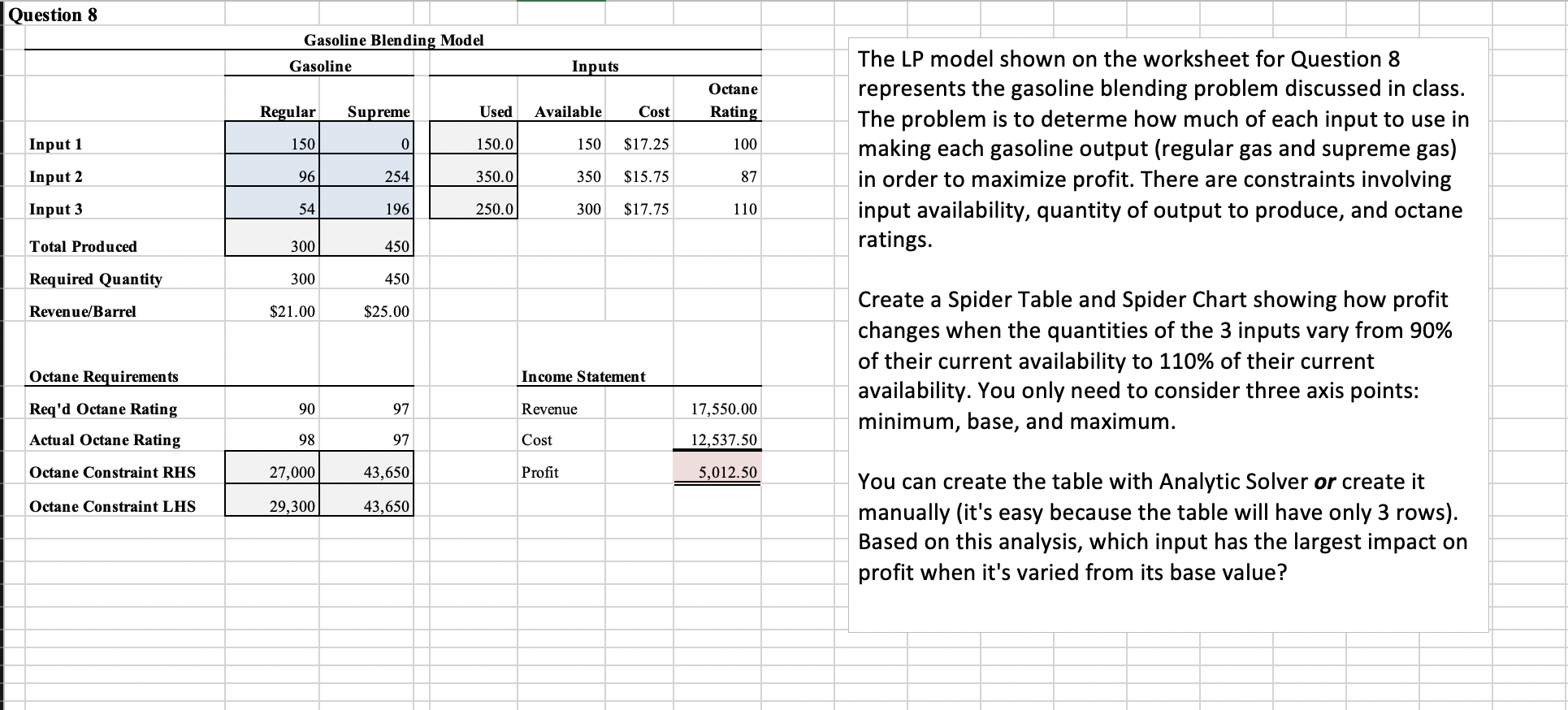
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


