Question:

Hello! I do not understand what the following question asks for a. subquestion. I feel confused. Can someone provide me with a detailed explanation? Thank you!

1. Go to the All Locations worksheet, where Benicio wants to summarize the quarterly and annual totals from the three locations for each type of product.

Consolidate the sales data from the three locations as follows:

a. In cell B5, enter a formula using the SUM function and 3-D references that totals the Mini sales values (cell B5) in Quarter 1 from the U.S., Canada, and Mexico worksheets.

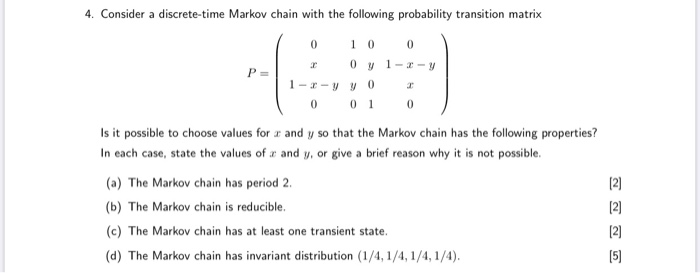
4. Consider a discrete-time Markov chain with the following probability transition matrix 0 0 0 0 7 1-3-y P = 1-I-VVO T 0 0 1 0 Is it possible to choose values for a and y so that the Markov chain has the following properties? In each case, state the values of a and y, or give a brief reason why it is not possible. (a) The Markov chain has period 2. [2) (b) The Markov chain is reducible. (c) The Markov chain has at least one transient state. UNN (d) The Markov chain has invariant distribution (1/4, 1/4, 1/4, 1/4).Consider a Markov chain {Xn : n = 0, 1, 2, ...} with state space {1, 2, 3} and one-step transition probability matrix O NIH NIH P = O 0 O (a) Mark O or X: ( ) The Markov chain is irreducible. ( ) The Markov chain is aperiodic. ( ) The Markov chain is transient. ( ) The Markov chain is recurrent. ( ) The Markov chain is null recurrent. ( ) The Markov chain is ergodic. (b) Calculate P(X5 = 1/X2 = 1). (c) Find limn + P(Xn = 1/X2 = 1).Problem 1. Consider the Markov chain with transition matrix 0.2 0.4 0 0.47 A = 0.3 0 0.7 0 0.5 0 0.5 0 0 0.1 0.9 O Which states are transient and which are recurrent? Is this Markov chain irreducible or reducible? What is its period? Problem 2. Consider the Markov chain with transition matrix A = [0.1 0.9 1 0 Which states are transient and which are recurrent? Is this Markov chain irreducible or reducible? What is its period? Find its stationary distribution and rate of convergence. Problem 4. Consider the Markov chain with transition matrix 0.5 0 0.5 A = 01 0 0.4 0 0.6 Which states are transient and which are recurrent? Is this Markov chain irreducible or reducible? What is its period? Find its stationary distributions.4. Consider the Markov chain X" = {X,} with state space S = {0, 1, 2, ...} and transition probabilities 1 ifj=i-1 Puj = 10 otherwise , for i 2 1 and Poo = 0, Poj = for j > 1. (a) Is this Markov chain irreducible? Determine the period for every state. (b) Is the Markov chain recurrent or transient? Explain. (c) Is the Markov chain positive recurrent? If so, compute the sta- tionary probability distribution. (d) For each state i, what is the expected number of steps to return to state i if the Markov chain X starts at state i? 5. Consider a Markov chain X = {X} with state space S = {0, 1, 2, ...} and transition probability matrix 0 1 0 0 P 0 0 P = O p 0 q 0 0 . . . 0 0 P 0 4 0 Here p > 0, q > 0 and p+q =1. Determine when the chain is positive recurrent and compute its stationary distribution