Question I:

You are given:

(i)Losses in a given year follow a Gamma distribution with parametersand, wheredoes not vary by policyholder.

(ii)The prior distribution ofhas mean 50.

(iii)The Buhlmann credibility factor based on two years of experience is 0.25.

CalculateVar().

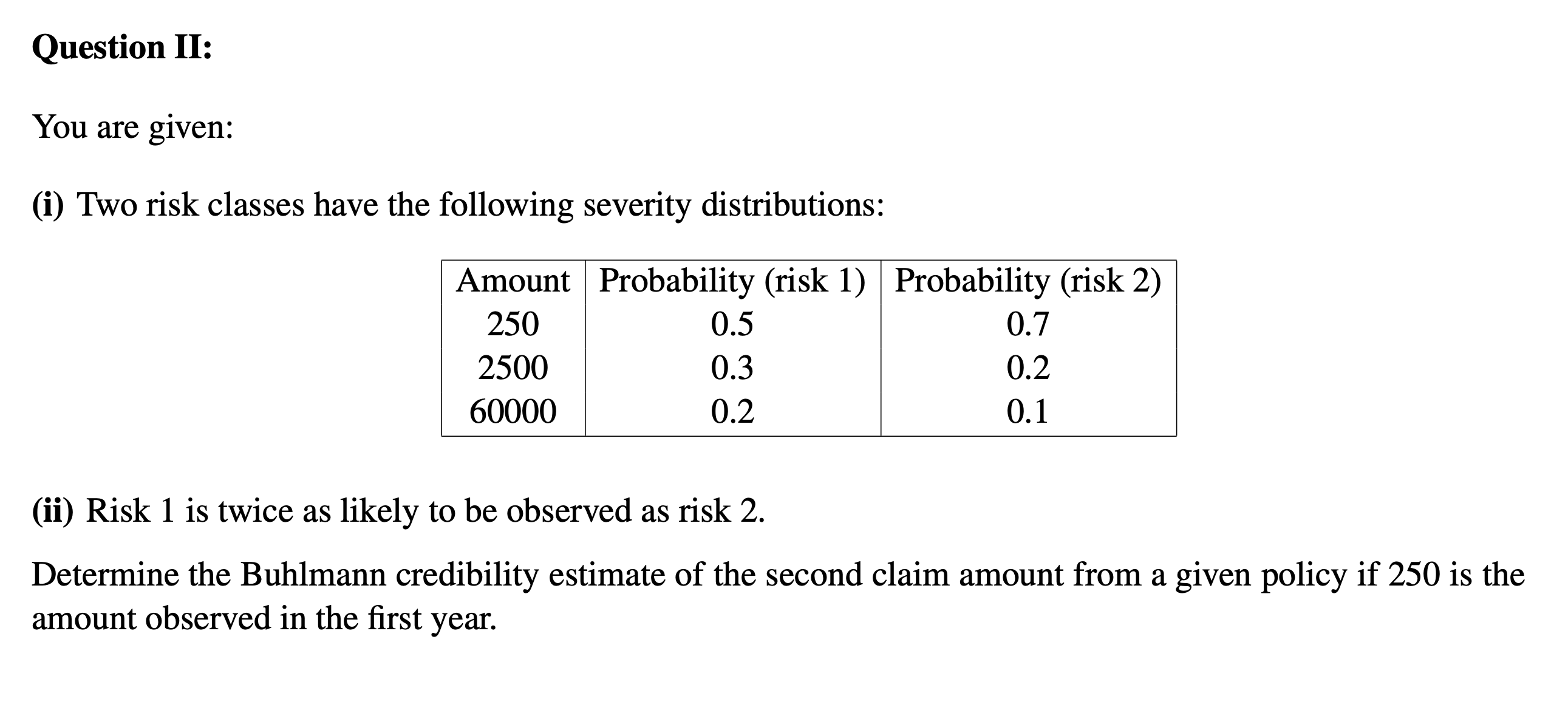
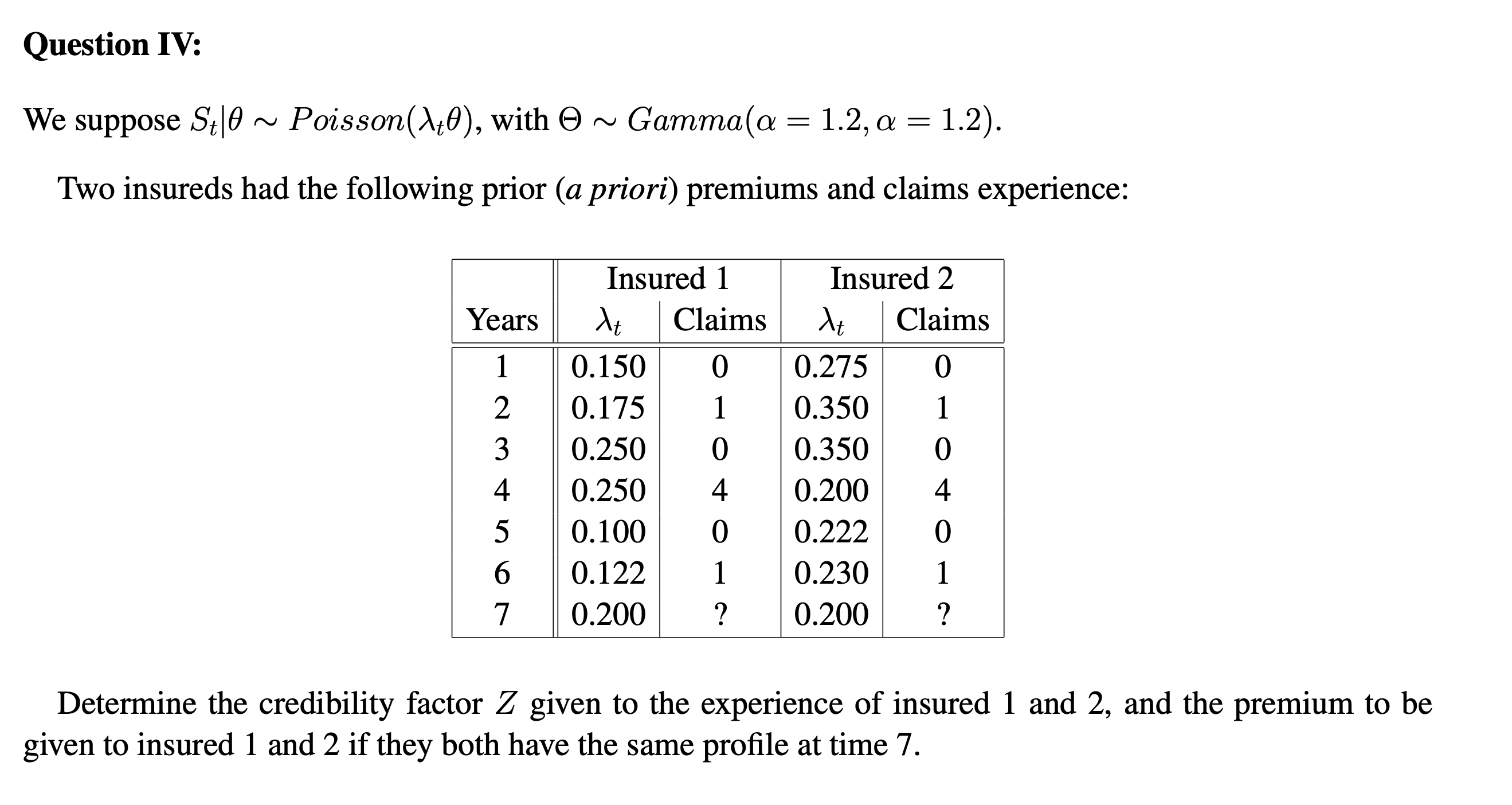
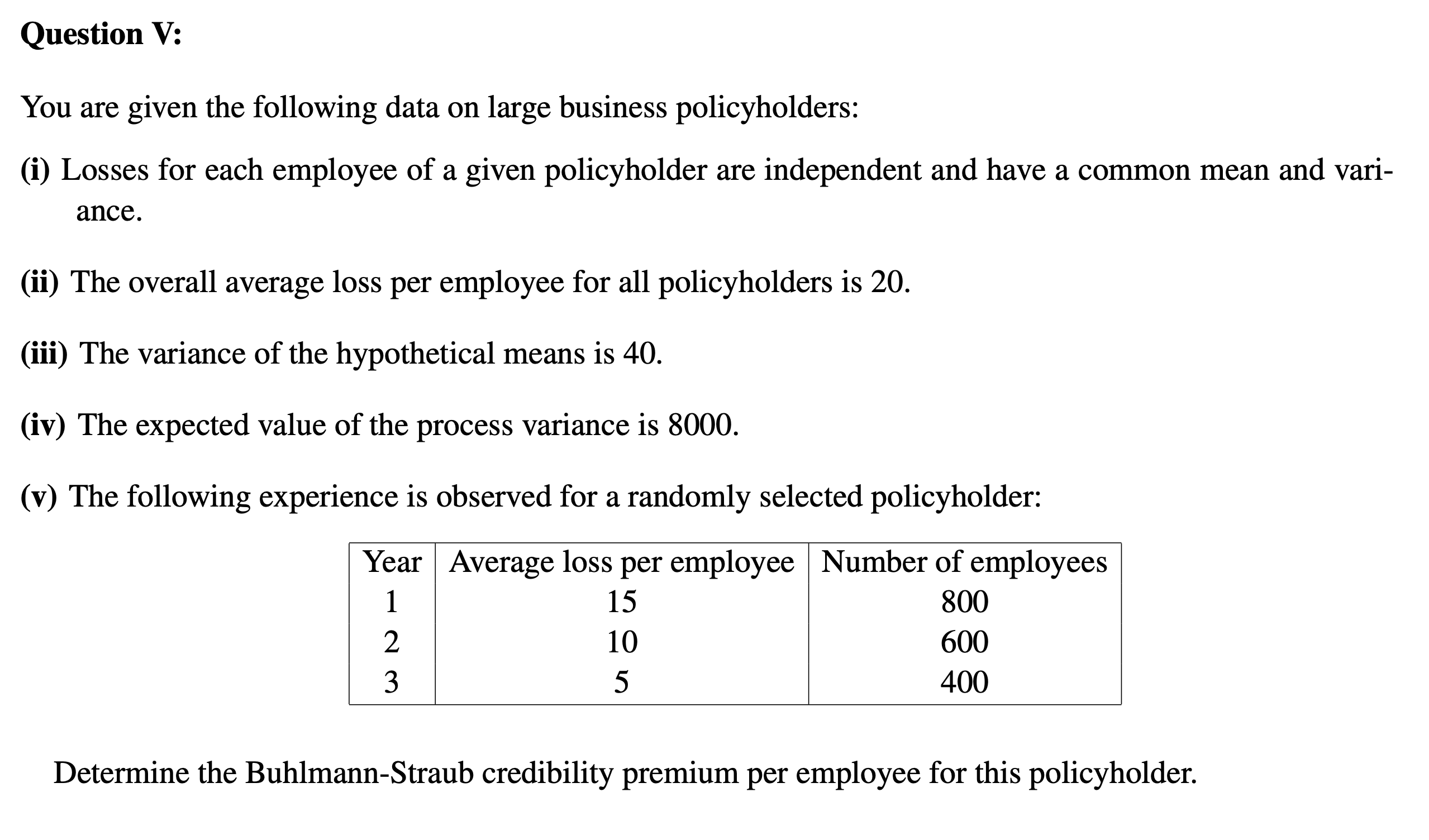
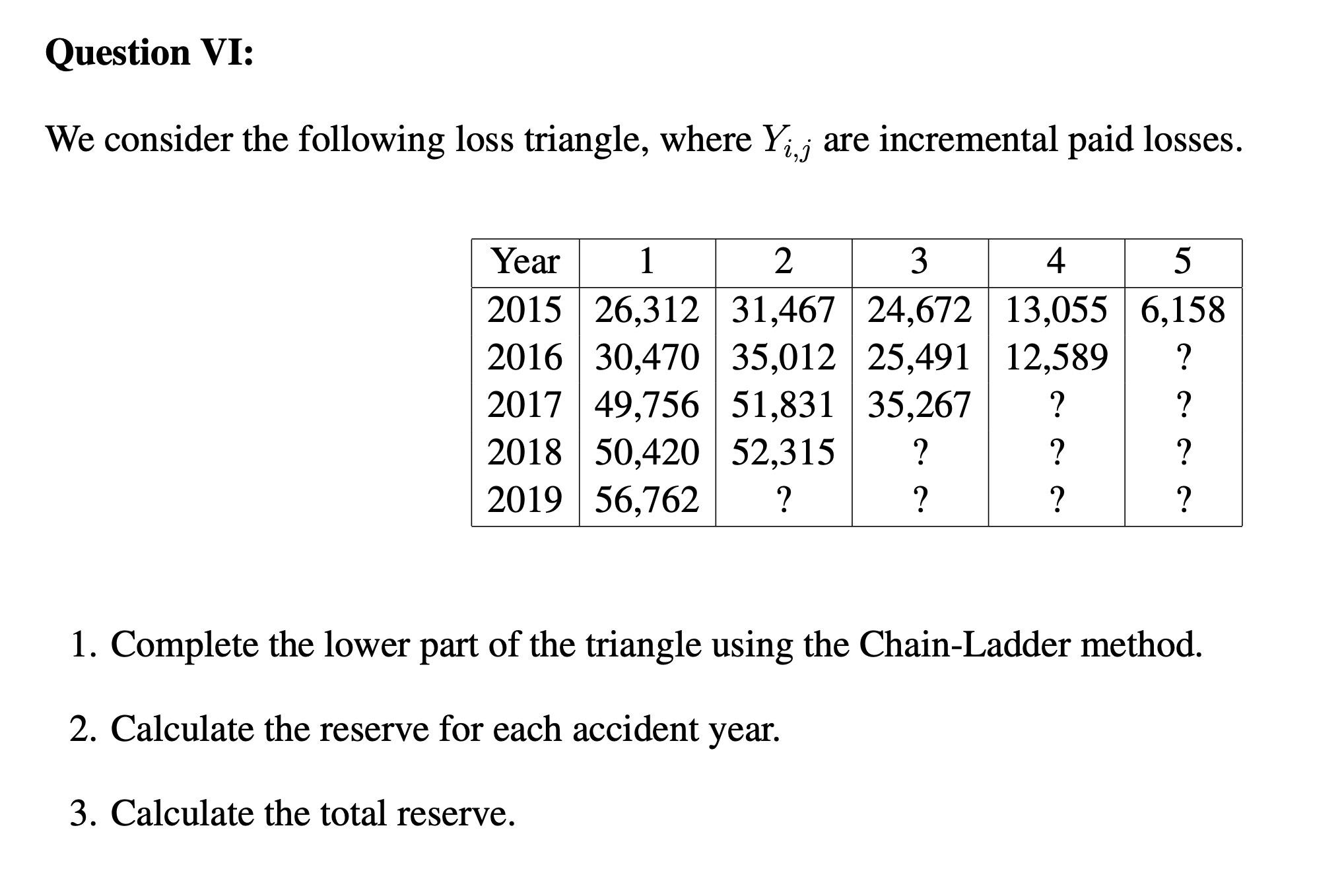
Question 11: You are given: (i) Two risk classes have the following severity distributions: Amount Probability (risk 1) Probability (risk 2) 250 0.5 0.7 2500 0.3 0.2 60000 0.2 0.1 (ii) Risk 1 is twice as likely to be observed as risk 2. Determine the Buhlmann credibility estimate of the second claim amount from a given policy if 250 is the amount observed in the rst year. Question III: We consider the Poisson-Gamma model, with the following assumptions: . Nit bi ~ Poisson(Niti) . Oi ~ Gamma(a, a) Show that the Buhlmann-Straub premium can be obtained as follows: Pir+1 = hit Et Nit + a Et ditt aQuestion IV: We suppose St|0 ~ Poisson()\\t0), with 6) ~ Gamma(a = 1.2, a = 1.2). Two insureds had the following prior (a priori) premiums and claims experience: Insured 1 Insured 2 Years At Claims At Claims 1 0.150 0 0.275 0 2 0.175 1 0.350 1 3 0.250 0 0.350 0 4 0.250 4 0.200 4 5 0.100 0 0.222 0 6 0.122 1 0.230 1 7 0.200 ? 0.200 ? Determine the credibility factor Z given to the experience of insured 1 and 2, and the premium to be given to insured 1 and 2 if they both have the same prole at time 7. Question V: You are given the following data on large business policyholders: (i) Losses for each employee of a given policyholder are independent and have a common mean and vari- ance. (ii) The overall average loss per employee for all policyholders is 20. (iii) The variance of the hypothetical means is 40. (iv) The expected value of the process variance is 8000. (v) The following experience is observed for a randomly selected policyholder: Year Average loss per employee Number of employees 1 15 800 2 10 600 3 5 400 Determine the Buhlmann-Straub credibility premium per employee for this policyholder. Question VI: We consider the following loss triangle, where YM- are incremental paid losses. 1. Complete the lower part of the triangle using the Chain-Ladder method. 2. Calculate the reserve for each accident year. 3. Calculate the total reserve