Question: Question: Lete 1 = (1,0,0) T , e 2 = (0,1, 0) T , e 3 = (0,0,1) T be the standard basis of R

Question:

Lete₁= (1,0,0)^T, e₂= (0,1, 0)^T, e₃= (0,0,1)^Tbe the standard basis ofR³. Consider a linear mapT:R³->R³satisfying T(x, y, z)^T= (0,0,0)^Twhenever 2x-y+z= 0.

(a) Show thatT ((1/2, 0, -1)^T)= (0,0,0)^Tand T(0, 1, 1)^T= (0, 0, 0)^T.

(b) Justify whetherTis an isomorphism using result from (a).

(d) Use your results ofT(e₁), T(e₂), T(e₃) to determine the image of an arbitrary vector

(x, y, z)^T

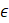
Question: Lete 1 = (1,0,0) T , e 2 = (0,1, 0) T ,

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Que1. Given the following code, what is the result when run? Select the one correct answer. public class Program { public static void main(String args [] ) { short eye = 1; short jay = 1; while (eye...

ushboard Site home Calendar Badges All courses Course dashboard Question 7 Which species is most likely to have multiple bonds? ot yet answered Select one: Marked out of 2.00 a. NH3 Fing question 0...

QUESTION 7 The equation of a particular electrical circuit is given by 20 d! + 80 di + = 0, if i(0) = 0 dt 0.01 and /'(0) =5. Determine the current at any time t > 0 and discuss the solution as t ->...

1. Consider the simple regression model: V/i = Po+ Piri +ui, for i = 1, ..., n, with E(ur,) 7 0 and let z be a dummy instrumental variable for a, such that we can write: with E(uilz;) = 0 and...

2. Consider the general linear model Y = XA + c, with : ~ N,,(0,o'I,, ), where the first column of X consists of all ones. (a) Using facts about the mean and variance/covariance of random vectors...

answer all questions as instructed below. make sure you have attended all questions .Comparative Architectures (a) Describe the organisation of a two-level branch predictor that makes use of a global...

Prepared by Gilberto Clavell Page 1 CHAPTER 3 PROJECT MANAGEMENT Chapter Abstract; The Project Manager is responsible for everything that is required to make the project a success - whether directly...

summarize this journal, the length of summary should not be more than 2 pages Journal of Banking & Finance 37 (2013) 578-586 Contents lists available at SciVerse ScienceDirect Journal of Banking &...

Please assist with the final exam. Please see the attached. FINC 340 INVESTMENTS FINAL EXAMINATION_04 DIRECTIONS: Here is the Final Examination Question Sheet. Please submit your Final Examination...

6. Finite Difference Method for 2D Elliptic PDEs (20 marks). (a) Implement a Matlab function with header function A=build laplace 2D (m) that constructs a sparse matrix A containing the 2D Laplacian...

Discuss the heroic attributes of Rustem. Is there anything about his characteristics that reminds you of current heroes? 1. Start by introducing, quoting, and discussing the following passage from...

Strong ethical relativism is the position that A. The individual must decide in any given situation what is right and wrong B. Might makes right C. All ethical rules are tied to ones particular...

Stepping an engagement down to a compilation from a review to avoid a disclosure issue shouldonly be considered by the accountant under which circumstance? A If he or she is convinced that the...

I need help with the following. The commercial airport terminal's passenger handling system is a series of links and processes that facilitate the transfer of passengers between an aircraft and one...