question :Please use WOLFRAM MATHEMATICA to get answer An employee has two tasks. Each produces an outcome. The first task affects the first and second outcome the second task affects only the second outcome. To formalize further, the employee can choose either effort H or Effort L on each task. The employer wants to motivate effort H on each task. Both the employee and employer are risk neutral with utility of money w = U(w) = w, but the employee must always be paid a non-negative wage. The cost in terms of utility for effort H is one for each task, the cost in terms of utility for effort L is 0 for each task. The relationship between effort and outcome is shown below where the outcome for a task can be good G or bad B. First Task good bad High effort (H) .9 .1 Low effort (L) .45 .55

Second Task

Effort Task 1 Effort Task 2 % of G % of B H H .9 .1 H L .55 .45 L H .4 .6 L L .2 .8 Please use WOLFRAM MATHEMATICA to get answer

a. Assume the employer can only observe outcomes and not effort, design the best contract that motivates H on both tasks. b. Maintain all the assumptions above except assume now the employer can only observe the outcome on the second task, design the best contract that motivates H on both tasks. c. Does it matter if the employer can observe the outcome on the first task? Explain in a few words

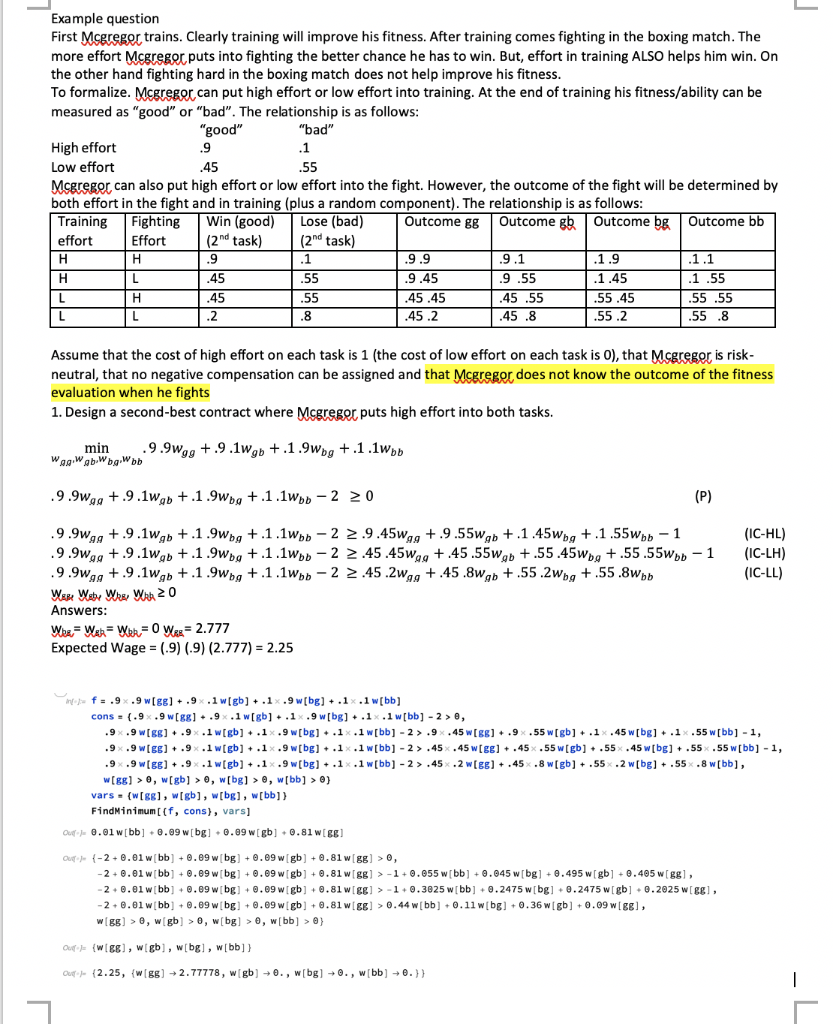
question : Please use WOLFRAM MATHEMATICA to get answer An employee has two tasks. Each produces an outcome. The first task affects the first and second outcome the second task affects only the second outcome. To formalize further, the employee can choose either effort H or Effort Lon each task. The employer wants to motivate effort H on each task. Both the employee and employer are risk neutral with utility of money w = U(w) = w, but the employee must always be paid a non-negative wage. The cost in terms of utility for effort H is one for each task, the cost in terms of utility for effort Lis O for each task. The relationship between effort and outcome is shown below where the outcome for a task can be good "G" or bad "B". First Task High effort (H) Low effort (L) "good" .9 .45 "bad" .1 .55 Second Task % of "G" % of "B" Effort Task 1 Effort Task 2 H H .9 .1 H L .55 .45 L H .4 .6 L L .2 .8 Please use WOLFRAM MATHEMATICA to get answer a. Assume the employer can only observe outcomes and not effort, design the best contract that motivates H on both tasks. b. Maintain all the assumptions above except assume now the employer can only observe the outcome on the second task, design the best contract that motivates H on both tasks. c. Does it matter if the employer can observe the outcome on the first task? Explain in a few words. "good" Example question First Mcgregor trains. Clearly training will improve his fitness. After training comes fighting in the boxing match. The more effort Megreger puts into fighting the better chance he has to win. But, effort in training ALSO helps him win. On the other hand fighting hard in the boxing match does not help improve his fitness. To formalize. Mcgregor can put high effort or low effort into training. At the end of training his fitness/ability can be measured as "good" or "bad". The relationship is as follows: "bad" High effort .9 .1 Low effort .45 .55 Mcgreger can also put high effort or low effort into the fight. However, the outcome of the fight will be determined by both effort in the fight and in training (plus a random component). The relationship is as follows: Training Fighting Win (good) Lose (bad) Outcome gg Outcome gb Outcome bg Outcome bb effort Effort (2nd task) (2nd task) H H .9 .1 .9.9 .9.1 .1.9 .1.1 H L .45 55 .9.45 .9.55 .1.45 .1.55 L H .45 .55 .45.45 .45 55 .55.45 .55 .55 L L .2 .8 .45.2 .45 .8 .55.2 .55.8 Assume that the cost of high effort on each task is 1 (the cost of low effort on each task is 0), that Mcgregor is risk- neutral, that no negative compensation can be assigned and that Mcgregor does not know the outcome of the fitness evaluation when he fights 1. Design a second-best contract where Msgreger puts high effort into both tasks. min .9.9wgg +.9.1wgb +.1.9wbg +.1.1wpb WagwgbWbg.Wbb .9.9wag +.9.1wgb +.1.9wbg +.1.1wbb - 2 2 0 (P) (IC-HL) (IC-LH) (IC-LL) .9.9wgg +.9.1wgb +.1.9wbg +.1.1wbb - 2 2.9.45wgg +.9.55w.gb +.1.45wbg +.1.55wbb - 1 9.9wgg +.9.1wgb +.1.9wbg +.1.1wbb - 2 2.45.45wag +.45.55w gb +.55.45wbg +.55.55wbb - 1 9.9wgg +.9.1wgb +.1.9wbg +.1.1wbb -2 2.45.2wag +.45.8w.gb +.55.2wbg +.55.8wbb Were Wety Who Wak 20 Answers: Wher Wer=Wkk = 0 Wes=2.777 Expected Wage = (-9) (-9) (2.777) = 2.25 ef=.9%.9 w[88] +.9%.1w[gb] + .1%.9 w[bg] + .1x.1w[bb] cons = {.9%.9 w[88] + .9.1w[gb] + .1%.9 w[bg] + .1%.1w[bb] - 2 > 0, .9%.9 [88] + .9%.1w[gb] + .1.9 w[bg] + .1.1w[bb] - 2 >.9%.45 w[88] + .9%.55 w[gb] + .1 .45 w[bg] + .1%.55 w[bb] -1, .9%.9 [88] + .9%.1w[gb] + .1.9 w[bg] + .lx.lw[bb] -2 > .45.45 w[88] + .45%.55 w[gb] + .55.45 w[bg] + .55.55 w[bb] -1, .9%.9 [88] + .9%.1w[gb] + .1%.9 w[bg] + .1.1w[bb] -2 > .45 .2 [88] + .45.8w[gb] + .55.2 w[bg] + .55.8 w[bb], w[8g) > 0, W[gb] > 0, w[bg] > 0, w[bb] > } vars= (w[88], w[gb], w[bg], [bb]) FindMinimum[{f, cons), vars] Oud-0.01 w[bb] +0.09 w[bg] +0.89 w[gb] +0.81 W[68] Our {-2 +0.01 wbb) + 0.69 w[bg] +0.09 w [gb] +0.81 w gg) >, - 2 + 0.01 w[bb] +0.89 w[bg] +0.09 w[gb] +0.81 wiggl > -1 + 0.655 w[bb] +0.645 w[bg] +0.495 w[gb] +0.405 w[ggl, -2 + 0.01 w[bb] +0.89 w[bg] +0.69 w[gb] +0.81 w[] > -1 +0.3625 w[bb] +0.2475 w[bg] +0.2475 w[gb] + 0.2025 w[g], -2 + 0.01 wbb] +0.69 w[bg] +0.69 w[gb] +0.81 W[] > 0.44 w[bb] +0.11 w[bg] +0.36w[gb] +0.09 w[88], W[88] > 0, w[gb] > 0, w[bg] > 0, w[bb] >0} Oulf (WIRE), W[gb], w[bg], w[bb]} Cu (2.25, {W[88] +2.77778, W[gb] +0., W[bg] +0., w[bb] +0.}} 1 question : Please use WOLFRAM MATHEMATICA to get answer An employee has two tasks. Each produces an outcome. The first task affects the first and second outcome the second task affects only the second outcome. To formalize further, the employee can choose either effort H or Effort Lon each task. The employer wants to motivate effort H on each task. Both the employee and employer are risk neutral with utility of money w = U(w) = w, but the employee must always be paid a non-negative wage. The cost in terms of utility for effort H is one for each task, the cost in terms of utility for effort Lis O for each task. The relationship between effort and outcome is shown below where the outcome for a task can be good "G" or bad "B". First Task High effort (H) Low effort (L) "good" .9 .45 "bad" .1 .55 Second Task % of "G" % of "B" Effort Task 1 Effort Task 2 H H .9 .1 H L .55 .45 L H .4 .6 L L .2 .8 Please use WOLFRAM MATHEMATICA to get answer a. Assume the employer can only observe outcomes and not effort, design the best contract that motivates H on both tasks. b. Maintain all the assumptions above except assume now the employer can only observe the outcome on the second task, design the best contract that motivates H on both tasks. c. Does it matter if the employer can observe the outcome on the first task? Explain in a few words. "good" Example question First Mcgregor trains. Clearly training will improve his fitness. After training comes fighting in the boxing match. The more effort Megreger puts into fighting the better chance he has to win. But, effort in training ALSO helps him win. On the other hand fighting hard in the boxing match does not help improve his fitness. To formalize. Mcgregor can put high effort or low effort into training. At the end of training his fitness/ability can be measured as "good" or "bad". The relationship is as follows: "bad" High effort .9 .1 Low effort .45 .55 Mcgreger can also put high effort or low effort into the fight. However, the outcome of the fight will be determined by both effort in the fight and in training (plus a random component). The relationship is as follows: Training Fighting Win (good) Lose (bad) Outcome gg Outcome gb Outcome bg Outcome bb effort Effort (2nd task) (2nd task) H H .9 .1 .9.9 .9.1 .1.9 .1.1 H L .45 55 .9.45 .9.55 .1.45 .1.55 L H .45 .55 .45.45 .45 55 .55.45 .55 .55 L L .2 .8 .45.2 .45 .8 .55.2 .55.8 Assume that the cost of high effort on each task is 1 (the cost of low effort on each task is 0), that Mcgregor is risk- neutral, that no negative compensation can be assigned and that Mcgregor does not know the outcome of the fitness evaluation when he fights 1. Design a second-best contract where Msgreger puts high effort into both tasks. min .9.9wgg +.9.1wgb +.1.9wbg +.1.1wpb WagwgbWbg.Wbb .9.9wag +.9.1wgb +.1.9wbg +.1.1wbb - 2 2 0 (P) (IC-HL) (IC-LH) (IC-LL) .9.9wgg +.9.1wgb +.1.9wbg +.1.1wbb - 2 2.9.45wgg +.9.55w.gb +.1.45wbg +.1.55wbb - 1 9.9wgg +.9.1wgb +.1.9wbg +.1.1wbb - 2 2.45.45wag +.45.55w gb +.55.45wbg +.55.55wbb - 1 9.9wgg +.9.1wgb +.1.9wbg +.1.1wbb -2 2.45.2wag +.45.8w.gb +.55.2wbg +.55.8wbb Were Wety Who Wak 20 Answers: Wher Wer=Wkk = 0 Wes=2.777 Expected Wage = (-9) (-9) (2.777) = 2.25 ef=.9%.9 w[88] +.9%.1w[gb] + .1%.9 w[bg] + .1x.1w[bb] cons = {.9%.9 w[88] + .9.1w[gb] + .1%.9 w[bg] + .1%.1w[bb] - 2 > 0, .9%.9 [88] + .9%.1w[gb] + .1.9 w[bg] + .1.1w[bb] - 2 >.9%.45 w[88] + .9%.55 w[gb] + .1 .45 w[bg] + .1%.55 w[bb] -1, .9%.9 [88] + .9%.1w[gb] + .1.9 w[bg] + .lx.lw[bb] -2 > .45.45 w[88] + .45%.55 w[gb] + .55.45 w[bg] + .55.55 w[bb] -1, .9%.9 [88] + .9%.1w[gb] + .1%.9 w[bg] + .1.1w[bb] -2 > .45 .2 [88] + .45.8w[gb] + .55.2 w[bg] + .55.8 w[bb], w[8g) > 0, W[gb] > 0, w[bg] > 0, w[bb] > } vars= (w[88], w[gb], w[bg], [bb]) FindMinimum[{f, cons), vars] Oud-0.01 w[bb] +0.09 w[bg] +0.89 w[gb] +0.81 W[68] Our {-2 +0.01 wbb) + 0.69 w[bg] +0.09 w [gb] +0.81 w gg) >, - 2 + 0.01 w[bb] +0.89 w[bg] +0.09 w[gb] +0.81 wiggl > -1 + 0.655 w[bb] +0.645 w[bg] +0.495 w[gb] +0.405 w[ggl, -2 + 0.01 w[bb] +0.89 w[bg] +0.69 w[gb] +0.81 w[] > -1 +0.3625 w[bb] +0.2475 w[bg] +0.2475 w[gb] + 0.2025 w[g], -2 + 0.01 wbb] +0.69 w[bg] +0.69 w[gb] +0.81 W[] > 0.44 w[bb] +0.11 w[bg] +0.36w[gb] +0.09 w[88], W[88] > 0, w[gb] > 0, w[bg] > 0, w[bb] >0} Oulf (WIRE), W[gb], w[bg], w[bb]} Cu (2.25, {W[88] +2.77778, W[gb] +0., W[bg] +0., w[bb] +0.}} 1