read and solve

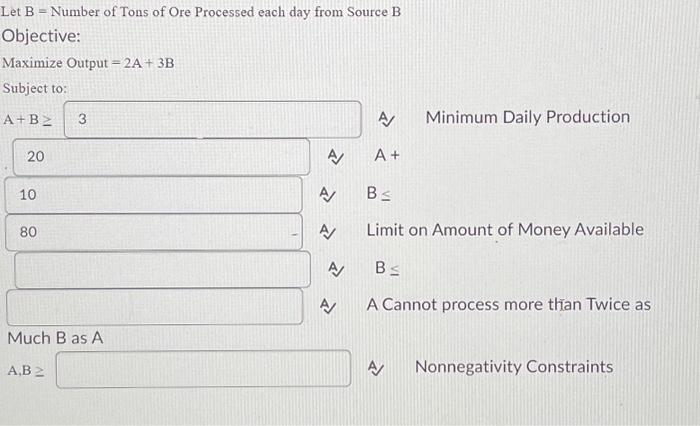
A gold processor has two sources of gold ore, source A and source B. In order to keep his plant running, at least three tons of ore must be processed each day. Ore from source A costs $20 per ton to process, and ore from source B costs $10 per ton to process. Costs must be kept to less than $80 per day. Moreover, Federal Regulations require that the amount of ore from source B cannot exceed twice the amount of ore from source A. If ore from source A yields 2oz. of gold per ton, and ore from source B yields 3oz. of gold per ton, how many tons of ore from both sources must be processed each day to maximize the amount of gold extracted subject to the above constraints? Let A= Number of Tons of Ore Processed each day from Source A Let B= Number of Tons of Ore Processed each day from Source B Objective: Maximize Output =2A+3B Let B = Number of Tons of Ore Processed each day from Source B Objective: Maximize Output =2A+3B Subject to: A+B A Minimum Daily Production A A+ A) B A Limit on Amount of Money Available A) B A A Cannot process more thian Twice as Much B as A A,B A Nonnegativity Constraints