Read the problem carefully. Draw a diagram if possible.

$2)$ DEFINE IN WORDS a variable for the quantity that is to be maximized or minimized. Also define variables to

represent the other unknown quantities.

$3)$ Write a formula for a target function $-$ a function for the quantity you wish to maximize or minimize.

$4)$ If it is a function of more than one variable, find equations that relate those variables. Use these equations to

eliminate all but one of the variables in your target function.

$5)$ Find derivative. Find critical points.

$6)$ Finding critical points isn$$t enough, you must justify that your answer is a maximum or minimum. If your

domain is a closed interval, you can use the Closed Interval Method. If not, you can use the First or Second

Derivative test.

$7)$ State your answer IN A SENTENCE with a correct unit of measure. Make sure you answer the question, and

check that your answer is reasonable. Put a box around your final answer.

$2.(4$ pts$)$ Find the maximum area of a rectangle inscribed between the $\backslash ($ x $\backslash )-$axis and the function $\backslash ($ f$($x$)=-$x$^\{4\}+3\backslash ).$

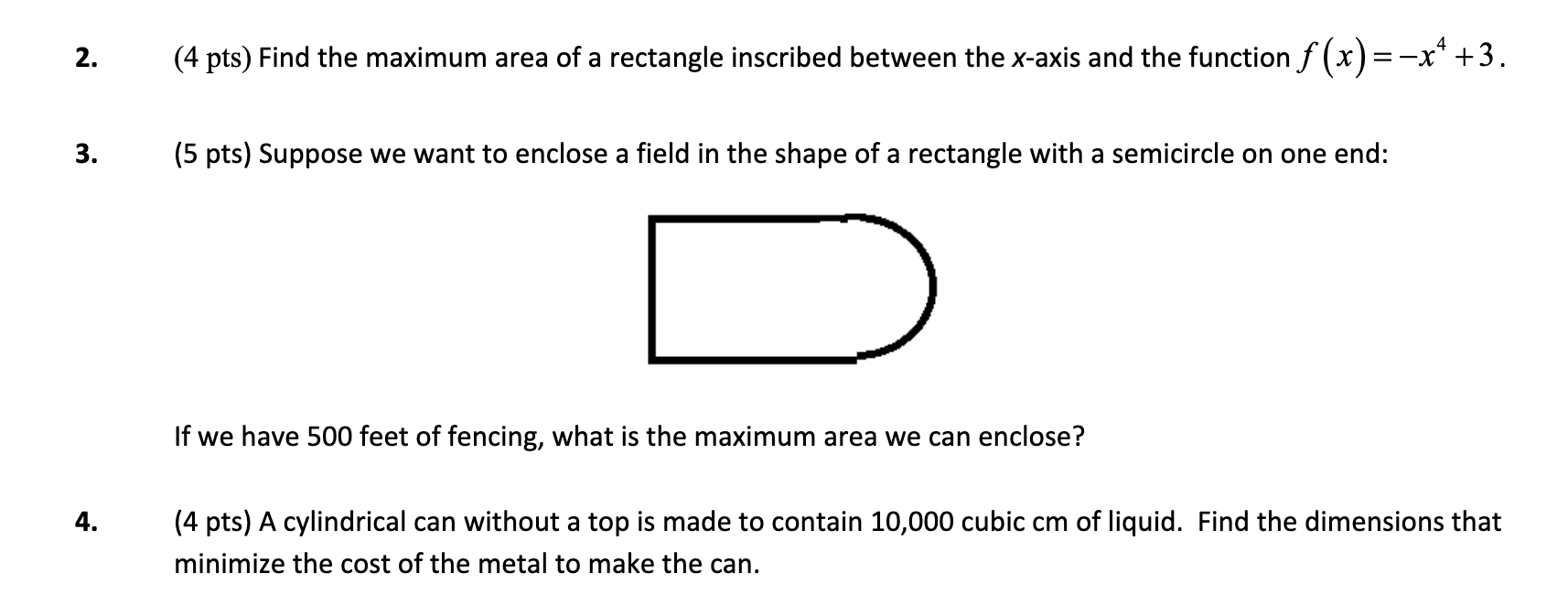
$3.(5$ pts$)$ Suppose we want to enclose a field in the shape of a rectangle with a semicircle on one end:

If we have $500$ feet of fencing, what is the maximum area we can enclose?

$4.(4$ pts$)$ A cylindrical can without a top is made to contain $10,000$ cubic cm of liquid. Find the dimensions that minimize the cost of the metal to make the can.