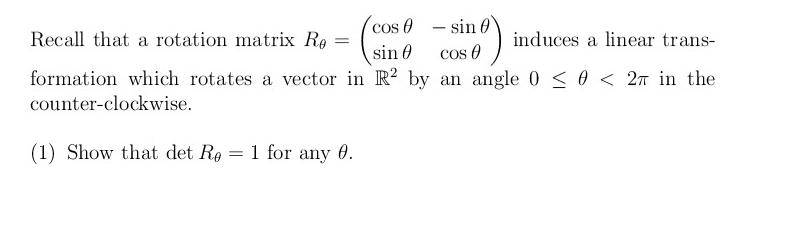
Recall that a rotation matrix Re (sind) induces a linear trans- sin 0 formation which rotates a vector in R2 by an angle 0 0 < 2 in the counter-clockwise. = (1) Show that det Re 1 for any 0. = cos - sin Let SO(2, R) {A M(R) | A- = At and det(A) = 1} be the set of special orthogonal matrices. Show that if A E SO(2, R), then A = Ro equals to a rotation matrix for some 0 0 < 2. = (3) Show that the rotation matrix R/2 has no real eigenvalue. (4) Find all the possible values for 0 0 < 2 such that the rotation matrix Re has a real eigenvalue. If it is the case, find all the real eigenvalues and corresponding eigenvectors (in R).