Rotations have various applications. We show in this project how they can be handled by matrices.

(a) Show that the linear transformation y = Ax with

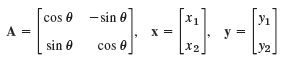is a counterclockwise rotation of the Cartesian x₁x₂-coordinate system in the plane about the origin, where θ is the angle of rotation.

(b) Show that in (a)

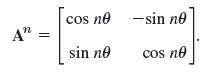
Is this plausible? Explain this in words.

(c) By geometry we should have

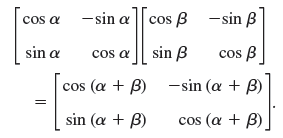
Derive from this the addition formulas (6) in App. A3.1.

(d) To visualize a three dimensional object with plane faces (e.g., a cube), we may store the position vectors of the vertices with respect to a suitable x₁x₂x₃-coordinate system (and a list of the connecting edges) and then obtain a two dimensional image on a video screen by projecting the object onto a coordinate plane, for instance, onto the x₁x₂-plane by setting x₃ = 0. To change the appearance of the image, we can impose a linear transformation on the position vectors stored. Show that a diagonal matrix D with main diagonal entries 3, 1, 1/2 gives from an x = [x_j] the new position vector y = Dx, where y₁ = 3x₁ (stretch in the x₁-direction by a factor 3), y₂ = x₂ (unchanged), y₃ = 1/2x₃ (contraction in the x₃-direction). What effect would a scalar matrix have?

(e) Explain y = Ax geometrically when A is one of the three matrices

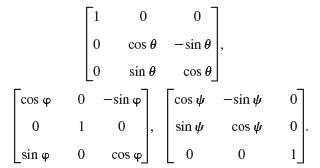
What effect would these transformations have in situations such as that described in (c)?

A = cos sin 0 -sin 0 cos X X1 X2 y = Y Y2