Question: Recall that for an operator L defined by Ly = Azy + Any' + Any for some functions Ap, Al, A2, the adjoint operator L*

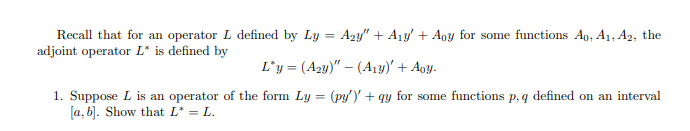
Recall that for an operator L defined by Ly = Azy" + Any' + Any for some functions Ap, Al, A2, the adjoint operator L* is defined by L'y = (Azy)" - (Aly)' + Any. 1. Suppose L is an operator of the form Ly = (py')' + qy for some functions p, q defined on an interval [a, b]. Show that L* = L

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

SOLVE Questions 1-5: PLEASE AND THANK YOU 1: What is the difference between homogenous and non-homogenous differential equation? Write an example for each and solve it. 2: What is the main formula to...

ESE 500: Homework 3 Due on October 16 (Monday) Part A: Matrix Exponential Problem 1. Without using Matlab, compute eAt , using two of your favourite methods, for: \u0014 \u0015 0 2 A= 1 2 It is...

Provide an appropriate query to show that the above program can give an incorrect result. [4 marks] (b) Explain the cause of the error. [6 marks] (c) Suggest a correction. [5 marks] (d) Write a...

Identify digital transformation theories mentioned in the article SMR JOURNAL OF SERVICE B 20280 MANAGEMENT RESEARCH SMR . Journal of Service Management Research . Issue 02/2018 EDITORS Digital...

Please answer all the questions. Thanks. Based on Exhibi 6-9 (Schedule A; Itemized deductions), Also attached: . 2017 Schedule A (same as Exhibit 6-9) 2018 Schedule A (draft) 2018 Schedule A...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

Please provide the summary of the methodology and your understanding of this paper. Incluse necessary figures as well. Rapid Object Detection using a Boosted Cascade of Simple Features single feature...

Write 2 paragraphs about Macro risks and the term structure of interest rates article. No max word count, page count, or formatting requirements but has to be submit to my tutor's work as my own....

Using the code provided in the photos attached, write the indicated code in signal.hxx (seen as the TODO portions) as seen in photos 2, 3, 4 so that it functions with the code in photo 1. Photos 5...

Mobey Chan He is now a senior audit manager in Westford & Co, a medium size CPA firm in Orange County. He works in the audit quality control department of the firm. His role includes performing...

Use structural induction to show that n(T) 2h(T) + 1, where T is a full binary tree, n(T) equals the number of vertices of T, and h(T) is the height of T.

Which of the following pieces of information, relating to the end investor, is critical to a financial advisor s financial plan design? Client s investment experience Client s risk tolerance Client s...

Prompt Imagine that you are looking for a job in digital marketing. What would your ideal position be? What type of company would you be interested in working for (think in terms of company size and...

2. In this chapter, the reader should reflect on the following concepts: Social facts, concrete fallacy, constructs, overestimation error.

1. Explain the following statements: a) Objective reality is always subjectively interpreted. b) What we know depends on whom we got to know it from.

4. Give examples from your everyday life where the process affects the result, but where the result also affects the process.