Question: Recall that HALT = { M , w : M halts on w } . Without loss of generality, we assume that the alphabet of
Recall that HALT M w : M halts on w Without loss of generality, we
assume that the alphabet of HALT is Sigma : q for some positive integer q For each nonnegative
integer n in N we define nq to be the baseq expansion of n so nq in q
Define
HALTLENGTH x in
: xq in HALT
a Prove that HALTLENGTH in PProblem points Recall that HALT halts on Without loss of generality, we
assume that the alphabet of HALT is :dots, for some positive integer For each nonnegative
integer ninN, we define :: to be the base expansion of so ::dots, Define
HALTLENGTH ::: HALT
a Prove that HALTLENGTH inP.
b Prove that HALTLENGTH PSIZE.
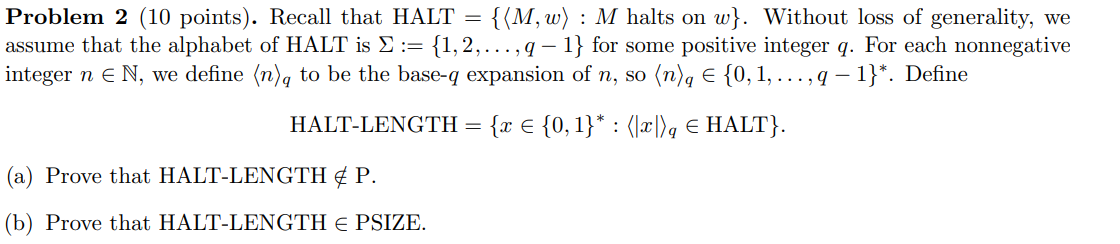
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


