Question: Recall the attributed grammar from question 1 Consider the following axiomatic semantics: {QID}ID>{Q}{QID,=0}{QID,=},issomeinteger {P1}S1ENDLINES2{Q}{P1}S1{P2},{P2}S2{Q},{Q+1}&{Q},{Q2}{Q},{P1}S1,S2{Q}{P1}S1{P2},{P2}S2{Q}{P1}S1ENDLINES2{Q}{P1}S2{P2},{P2}S1{Q}{Q+2}%{Q}{Q+ID}ID{Q} NOTE: The semantics in this questions is different from the one

Recall the attributed grammar from question 1 Consider the following axiomatic semantics:

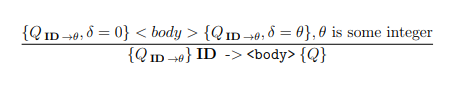
{QID}ID>{Q}{QID,=0}{QID,=},issomeinteger {P1}S1ENDLINES2{Q}{P1}S1{P2},{P2}S2{Q},{Q+1}&{Q},{Q2}{Q},{P1}S1,S2{Q}{P1}S1{P2},{P2}S2{Q}{P1}S1ENDLINES2{Q}{P1}S2{P2},{P2}S1{Q}{Q+2}%{Q}{Q+ID}ID{Q} NOTE: The semantics in this questions is different from the one presented in other questions. For the following program, assuming the precondition is \{\} , what is the value of main in the postcondition? Show the proof. main step, show step &&,& show %,&

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

The structural member is fabricated by welding two W130 x 28.1 sections together at an angle. Determine the maximum and minimum normal stresses acting on section m-n.

CS/CE 4337 Homework 01 Fall 2021 Homework 01 Answer the questions below, and submit electronically via elearning. Make sure you submit a couple hours early at the latest and double check your...

question 10 6. (10pts) Consider the following grammar: - - | ENDLINE ID ">" - | + ID | "&" "%" | 4." 8. (10pts) Recall the following grammar from question 6: (2) (3) | ENDLINE ID "->" | - ID 6 (5)...

question 11! 6. (10pts) Consider the following grammar: - - | ENDLINE ID ">" - | + ID | "&" "%" | 4." 8. (10pts) Recall the following grammar from question 6: (2) (3) | ENDLINE ID "->" | - ID 6 (5)...

need question 9 6. (10pts) Consider the following grammar: - - | ENDLINE ID ">" - | + ID | "&" "%" | 4." 8. (10pts) Recall the following grammar from question 6: (2) (3) | ENDLINE ID "->" | - ID 6...

11. (10pts) Recall the attributed grammar from question 8. Consider the following ax- iomatic semantics: {Q1D-0,8 = 0} {Q10 +0,8 = 0} {Q ID ---} ID -> {Q} {P1}S,{P2}, {P2}S,{Q} {PI}S, ENDLINE S,{Q}...

Recall the attributed grammar 3. (10pts) Recall the attributed grammar from question 11. Consider the following denotational semantics. bodysem("")=10 NOTE: The format is similar to our example from...

What is the critical path of a synchronous clock domain and how does it affect performance? [2 marks] (b) Name two tools that can be used for locating the critical paths of a system on chip before...

Recall the following grammar: Consider the following attribute computation functions and predicate functions: We constructed the attributed grammar to specify the details of the statement variables...

5. (20pt) Consider the following SLR(1) grammar G for arithmetic expressions: E EAT E T T TMF T F F -F F (E) A + - M F id (1) (15pt) Construct an attributed grammar, based on G, that computes the...

Find the natural lifetime in seconds for first-order reactions corresponding to (a) k = 0.497 s-1. (b) [A]0 = 3.16 M, and [A]t 5 0.496 M at t 5 3876 s. (c) half-life, t1/2, 5 26.5 years.

First Quarter Second Quarter Third Quarter Fourth Quarter Sales 1,673,200 1,673,200 1,723,396 Cost of Goods sold 1,070,848 1,070,848 1,070,848 Gross Profit Margin 602,352 602,352 652,548 Expenses...

A company has provided the following data concerning an irvestment project that it is considering: \ table [ [ Initial investment,$ , 1 6 0 , 0 0 0 ] , [ Annual cash flow,, ] , [ Salvage value at , ,...

Compared with half a century ago, adoption has become _ _ _ _ _ _ _ _ _ common, but it is more open and acceptabl e , so we probably discuss it _ _ _ _ _ _ _ . fill in the blanks more or much less or...

Critically evaluate: In comparing the two equilibrium positions in Figure 3.7b, I note that a smaller amount is actually demanded at a lower price. This refutes the law of demand.

ADVANCED ANALYSIS Assume that demand for a commodity is represented by the equation P 10 .2Qd and supply by the equation P 2 .2Qs, where Qd and Qs are quantity demanded and quantity supplied,...

LAST WORD What is the current overall number of American candidates waiting for an organ transplant? (For the answer, visit the United Network for Organ Sharing Web site, www.unos.org.) For what...