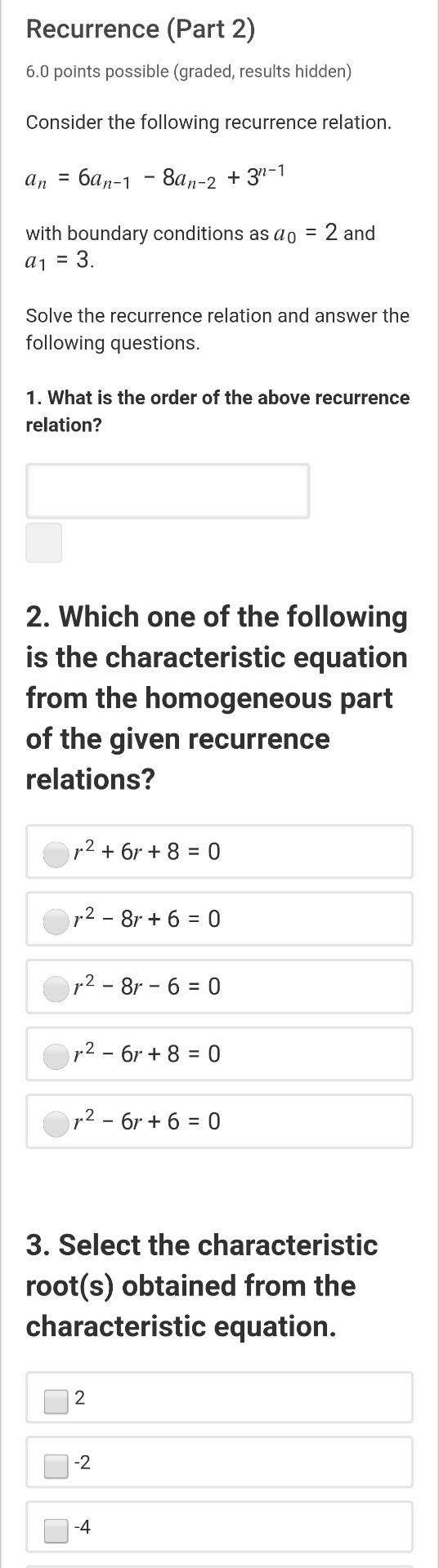
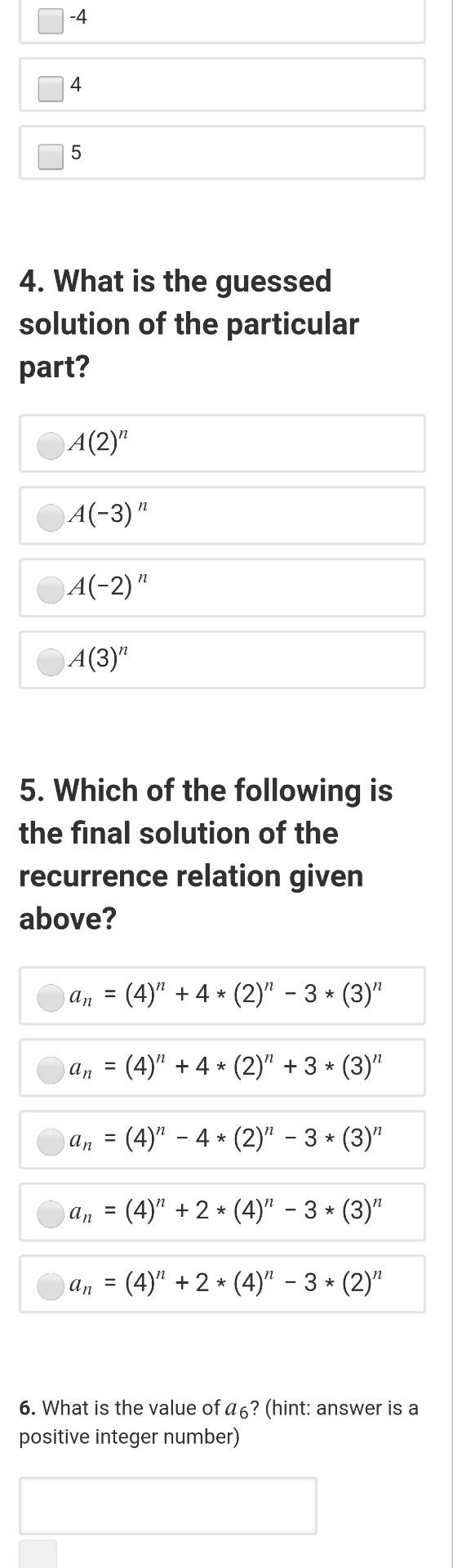
Recurrence (Part 2) 6.0 points possible (graded, results hidden) Consider the following recurrence relation. an = 6an-1 - 8an-2 + 31-1 with boundary conditions as do = 2 and a1 = 3. Solve the recurrence relation and answer the following questions. 1. What is the order of the above recurrence relation? 2. Which one of the following is the characteristic equation from the homogeneous part of the given recurrence relations? r2 + 6r + 8 = 0 p2 - 8r + 6 = 0 p2 - 8r - 6 = 0 r2 - 6r + 8 = 0 r2 - 6r + 6 = 0 3. Select the characteristic root(s) obtained from the characteristic equation. 2 -2 -4 -4 4 5 4. What is the guessed solution of the particular part? A(2)" n A(-3) " n A(-2) A(3)" 5. Which of the following is the final solution of the recurrence relation given above? an = (4) +4 * (2)" - 3* (3)" = an (4)" + 4 * (2)" + 3 * (3)" an = (4)" 4 * (2)" - 3* (3)" an (4)" + 2 * (4)" - 3* (3)" an = (4)" + 2 * (4)" - 3+ (2)" 6. What is the value of a6? (hint: answer is a positive integer number)