Refer to Fig. $4\mathrm{.}3.$ Prove mathematically that, all else being equal, the standard deviation of the response distribution is highest when $\backslash$sigma $=\backslash$sigma s

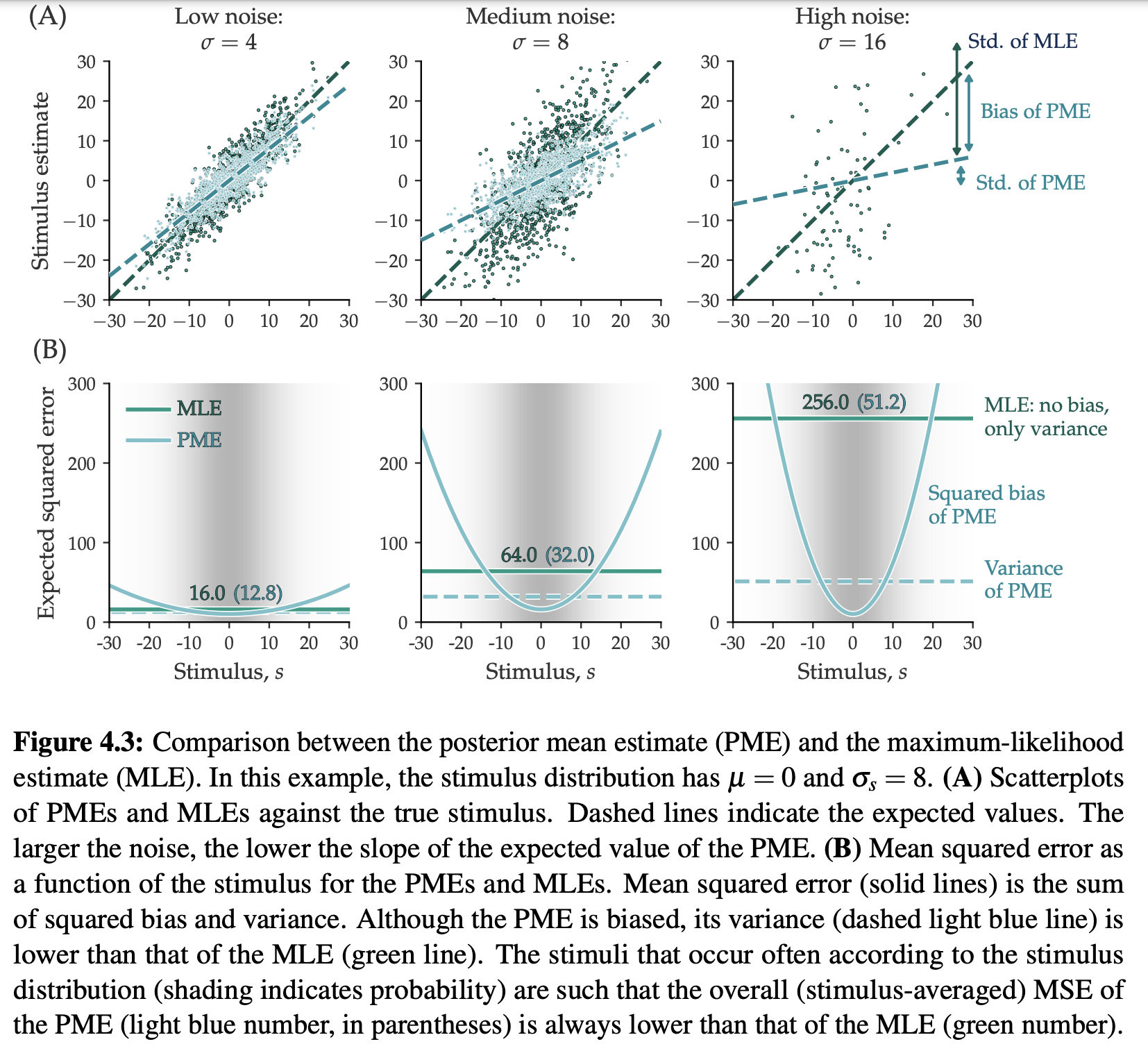
$.($Hint: at the maximum of a function, what is the value of the derivative?$).$ Figure $4\mathrm{.}3$: Comparison between the posterior mean estimate $($PME$)$ and the maximum$-$likelihood

estimate $($MLE$).$ In this example, the stimulus distribution has $=0$ and ${}_s=8.($A$)$ Scatterplots

of PMEs and MLEs against the true stimulus. Dashed lines indicate the expected values. The

larger the noise, the lower the slope of the expected value of the PME. $($B$)$ Mean squared error as

a function of the stimulus for the PMEs and MLEs. Mean squared error $($solid lines$)$ is the sum

of squared bias and variance. Although the PME is biased, its variance $($dashed light blue line$)$ is

lower than that of the MLE $($green line$).$ The stimuli that occur often according to the stimulus

distribution $($shading indicates probability$)$ are such that the overall $($stimulus$-$averaged$)$ MSE of

the PME $($light blue number, in parentheses$)$ is always lower than that of the MLE $($green number$).$