Refer to the image attached for question #2, (the analysis that has to be followed is above the purple line. )

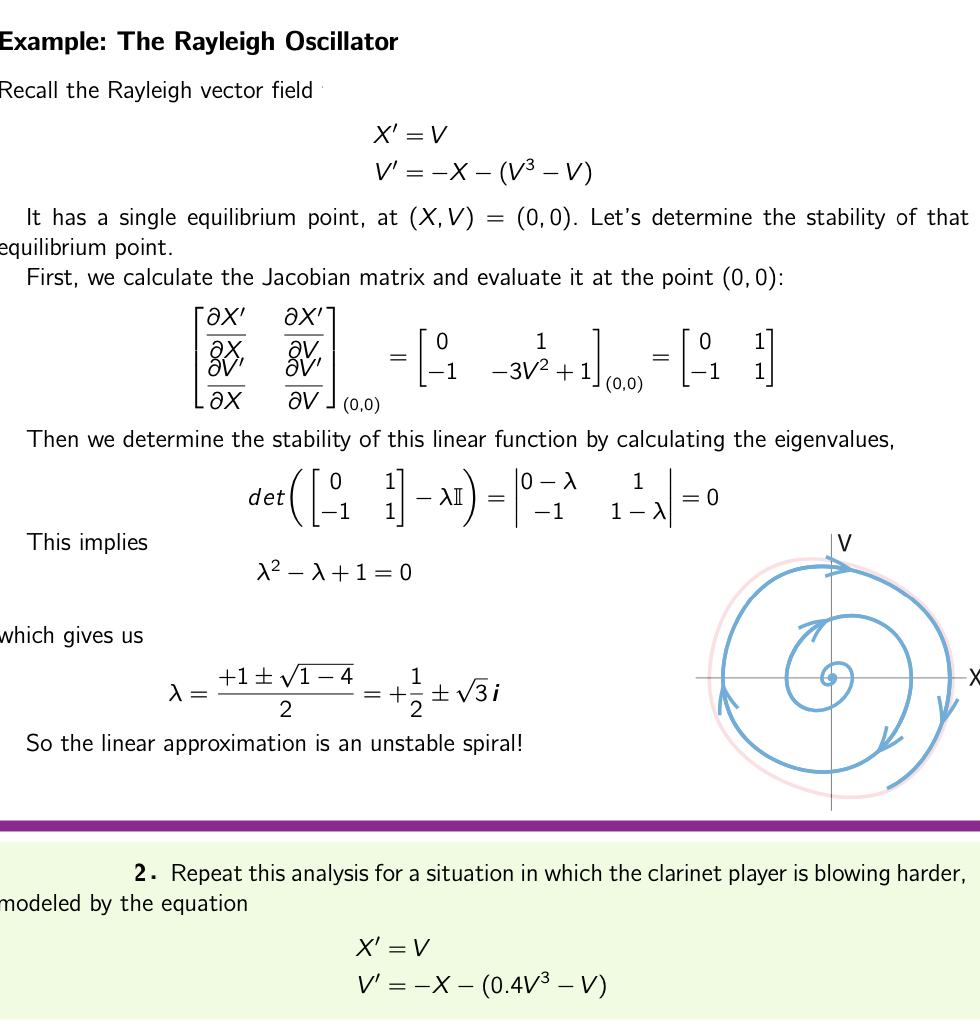
Example: The Rayleigh Oscillator Recall the Rayleigh vector field ' X" = V V' =X(v3V) It has a single equilibrium point, at (X. V) = (0.0). Let's determine the stability of that equilibrium point. First, we calculate the Jacobian matrix and evaluate it at the point (0,0): 6X' 6X' 7 = 0 1 = 0 1 gv' & [1 3v2 +1L0 D) [1 1 6X 6V (0.0) Then we determine the stability of this linear function by calculating the eigenvalues, 0 1 0 A 1 det([_1 1])\\I[) _1 1)'i0 This implies V A2 A + 1 = 0 which gives us 1 :l: x/l 4 1 A = + = + :l: \\/:' )4 2 2 So the linear approximation is an unstable spiral! 2 - Repeat this analysis for a situation in which the clarinet player is blowing harder, rnodeled by the equation X\" = v v' = X (0.4V3 V)