Reference: Calculus and Its Applications, 12th, by Marvin L. Bittinger and David Ellenbogen Book

Elementary Applied Calculus

I need help with questions

These are practice questions

Links to Book Below:

1. Calculus And Its Applications, Brief Version 12th edition | Print ISBN - 9780135164884, eText ISBN - 9780135225103 | VitalSource

2. Bittinger, Ellenbogen, Surgent & Kramer, Calculus and Its Applications: Brief Version, 12th Edition | Pearson

These are are practice questions

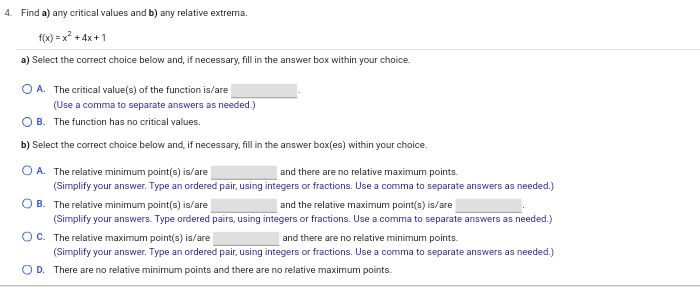
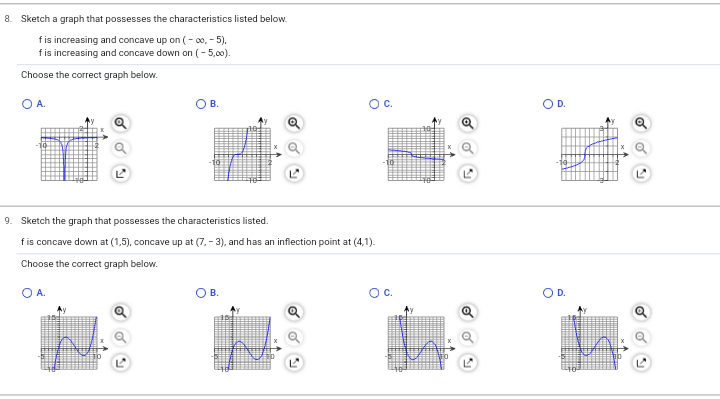
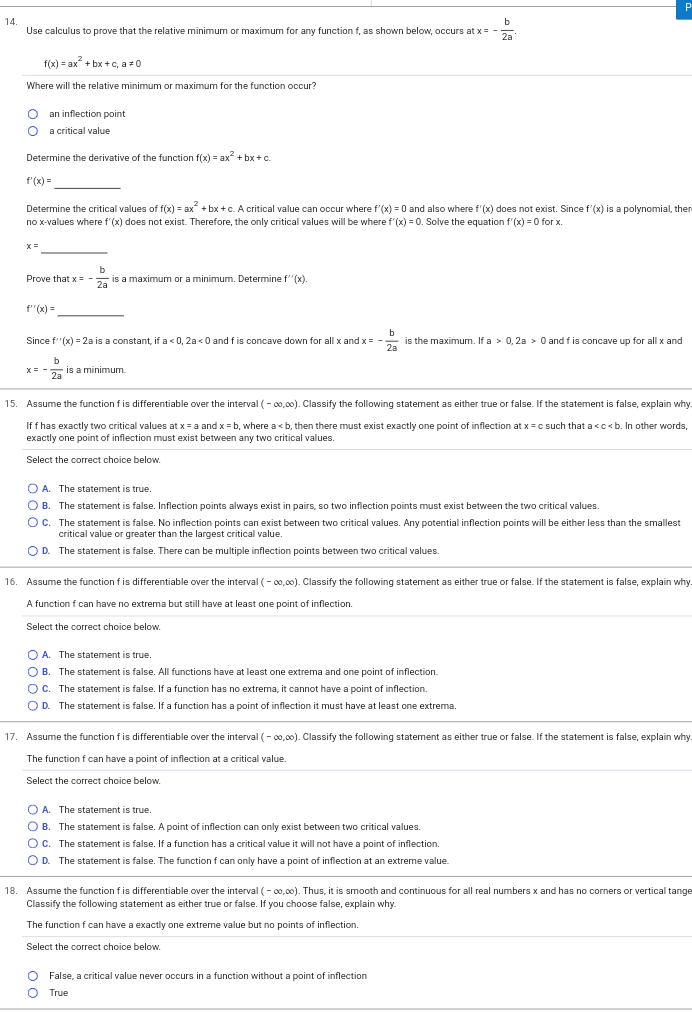
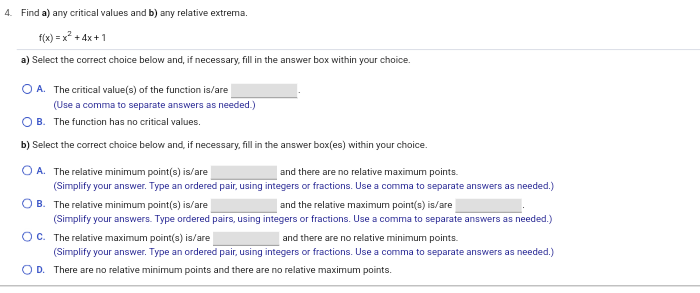
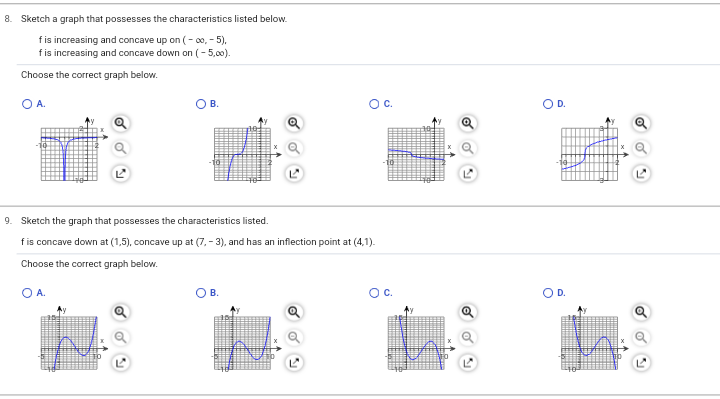
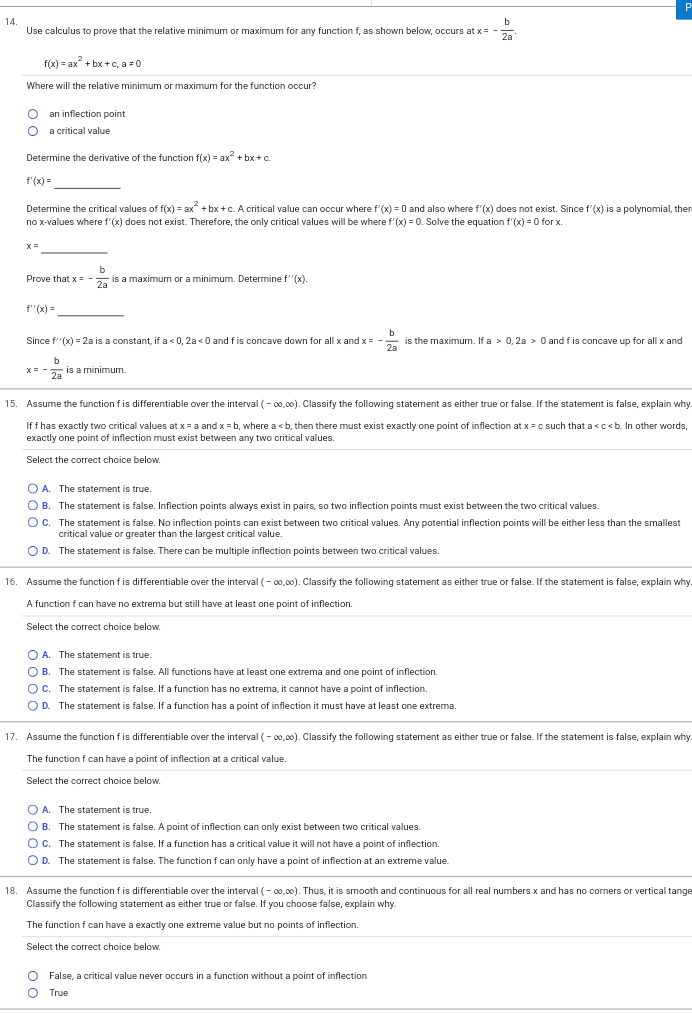
4. Find a) any critical values and b) any relative extrema. f (x) = x +4x+1 a) Select the correct choice below and, if necessary, fill in the answer box within your choice. O A. The critical value(s) of the function is/are (Use a comma to separate answers as needed.) O B. The function has no critical values. b) Select the correct choice below and, if necessary, fill in the answer box(es) within your choice. O A. The relative minimum point(s) is/are and there are no relative maximum points. (Simplify your answer. Type an ordered pair, using integers or fractions. Use a comma to separate answers as needed.) Q B. The relative minimum point(s) is/are and the relative maximum point(s) is/are (Simplify your answers. Type ordered pairs, using integers or fractions. Use a comma to separate answers as needed.) Q C. The relative maximum point(s) is/are and there are no relative minimum points. (Simplify your answer. Type an ordered pair, using integers or fractions. Use a comma to separate answers as needed.) O D. There are no relative minimum points and there are no relative maximum points.3. Use the Chain Rule to differentiate the following function. f(x) = (3x* + (5x -2)3)" f'(x) = 4. Find a) any critical values and b) any relative extrema. f(x) = x"+4x+1 a) Select the correct choice below and, if necessary, fill in the answer box within your choice. O A. The critical value(s) of the function is/are (Use a comma to separate answers as needed.) O B. The function has no critical values. b) Select the correct choice below and, if necessary, fill in the answer box(es) within your choice. O A. The relative minimum point(s) is/are and there are no relative maximum points. (Simplify your answer. Type an ordered pair, using integers or fractions. Use a comma to separate answers as needed.) B. The relative minimum point(s) is/are and the relative maximum point(s) is/are (Simplify your answers. Type ordered pairs, using integers or fractions. Use a comma to separate answers as needed.) O C. The relative maximum point(s) is/are and there are no relative minimum points. (Simplify your answer. Type an ordered pair, using integers or fractions. Use a comma to separate answers as needed.) O D. There are no relative minimum points and there are no relative maximum points. 5. Find a) any critical values and b) any relative extrema. g(x) = - x#+3x - 4 a) Select the correct choice below and, if necessary, fill in the answer box within your choice. O A. The critical value(s) of the function is/are (Use a comma to separate answers as needed.) B. The function has no critical values. b) Select the correct choice below and, if necessary, fill in the answer box(es) within your choice. A. The relative minimum point(s) is/are and the relative maximum point(s) is/are (Simplify your answers. Type ordered pairs, using integers or fractions. Use a comma to separate answers as needed.) O B. The relative maximum point(s) is/are and there are no relative minimum points. Simplify your answer. Type an ordered pair, using integers or fractions. Use a comma to separate answers as needed.) O C. The relative minimum point(s) is/are and there are no relative maximum points. (Simplify your answer. Type an ordered pair, using integers or fractions. Use a comma to separate answers as needed.) O D. There are no relative minimum points and there are no relative maximum points. 6. For the graph shown, identify a) the point(s) of inflection and b) the intervals where the function is concave up or concave down. a) The point(s) of inflection is/are (Type an ordered pair. Use a comma to separate answers as needed.) b) Identify the intervals where the function is concave up or concave down. The function is concave up on and concave down on (Simplify your answers. Type your answers in interval notation. Use a comma to separate answers as needed.)8. Sketch a graph that possesses the characteristics listed below. f is increasing and concave up on ( - 00, - 5), f is increasing and concave down on ( - 5,co). Choose the correct graph below. O A. OB. O C. O D. O LA LA 9. Sketch the graph that possesses the characteristics listed. f is concave down at (1,5), concave up at (7, - 3), and has an inflection point at (4,1). Choose the correct graph below. O A. OB. O C. OD. LA LA10. Sketch the graph that possesses the characteristics listed below. f'( - 2) = 0, f"'( - 2) 0, f(2) = - 5; f"(0) = 0, f(0) = - 2 Choose the correct graph below. OA O B. O c. OD Q Q Q Q 11. A person coughs when a foreign object is in the windpipe. The velocity of the cough depends on the size of the object. Suppose a person has a windpipe with 25-mm radius. If a foreign object has a radius r, in millimeters, then the velocity V, in millimeters/second, needed to remove the object by a cough is given by following equation, where k is some positive constant. For what size object is the maximum velocity needed to remove the object? vir) =k (25r2 -r3). Osrs 25 An object that has a radius of (1) will need maximum velocity to remove it. (Type an integer or a simplified fraction.) (1) O mm O mm 0 mm / second 12. The number of visitors P to a website in a given week over a 1-year period is given by P(t) = 124 + (t - 80) ed.", where t is the week and Ists 52. a) Over what interval of time during the 1-year period is the number of visitors decreasing? 6) Over what interval of time during the 1-year period is the number of visitors increasing? c) Find the critical point, and interpret its meaning. a) The number of visitors is decreasing over the interval (Simplify your answer. Type integers or decimals rounded to three decimal places as needed. Type your answer in interval notation.) b) The number of visitors is increasing over the interval Simplify your answer. Type integers or decimals rounded to three decimal places as needed. Type your answer in interval notation.) c) The critical point is (Type an ordered pair. Type integers or decimals rounded to three decimal places as needed.) Interpret what the critical point means. The critical point means that the number of visitors was (1) in week at approximately visitors. (Round to the nearest integer as needed.) (1) O maximized J minimized 13. Determine which graph is the derivative of the other and explain why. O A. The function p is the derivative of the function r because p = 0 at all values of x where r has an inflection point. B. The function p is the derivative of the function r because p = 0 at all values of x where r has a relative minimum or maximum. O C. The function r is the derivative of the function p because r = 0 at all values of x where p has a relative minimum or maximum. O D. Neither function could be the derivative of the other.14. Use calculus to prove that the relative minimum or maximum for any function f, as shown below, occurs at x = b f(x) = ax + bx + c, a = 0) Where will the relative minimum or maximum for the function occur? O an inflection point O a critical value Determine the derivative of the function f(x) = ax~+ bx + c. f (x) = Determine the critical values of f(x) = ax" + bx + C. A critical value can occur where f'(x) =0 and also where f'(x) does not exist. Since f'(x) is a polynomial, the no x-values where f'(x) does not exist. Therefore, the only critical values will be where f'(x) = 0. Solve the equation f'(x) = 0 for x. Prove that x = = = is a maximum or a minimum. Determine f" (x). f(x) = Since f" (x) = 2a is a constant, if a 0, 2a > 0 and f is concave up for all x and X = 2a Is a minimum. 15. Assume the function f is differentiable over the interval ( - co,co). Classify the following statement as either true or false. If the statement is false, explain why If f has exactly two critical values at x = a and x = b, where a