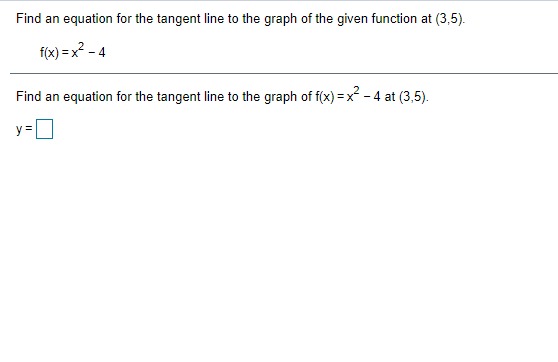
Reference: Calculus and Its Applications, 12th, by Marvin L. Bittinger and David Ellenbogen Book

Elementary Applied Calculus

I need help with questions

These are practice questions

Links to Book Below:

1. Calculus And Its Applications, Brief Version 12th edition | Print ISBN - 9780135164884, eText ISBN - 9780135225103 | VitalSource

2. Bittinger, Ellenbogen, Surgent & Kramer, Calculus and Its Applications: Brief Version, 12th Edition | Pearson

These are are practice questions

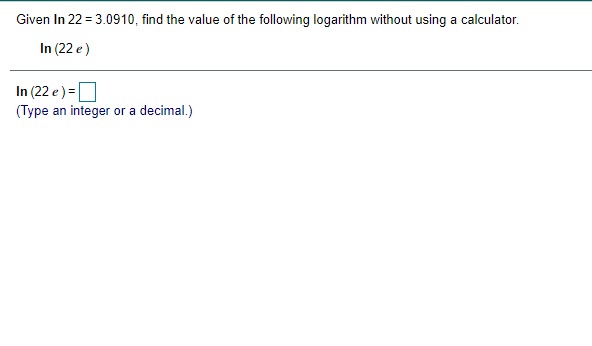
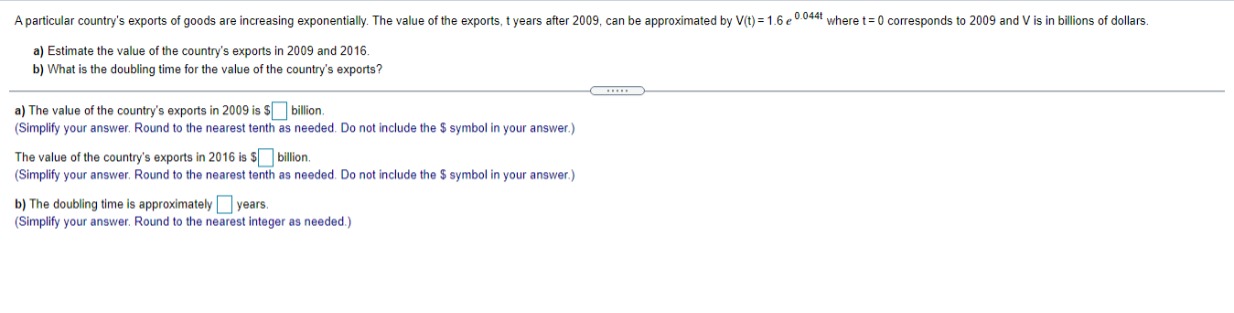
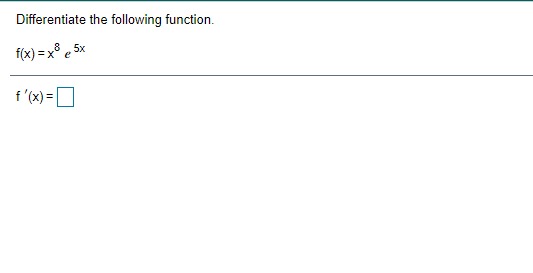
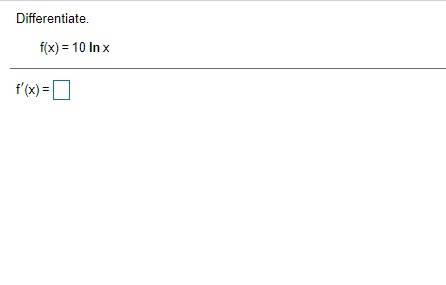
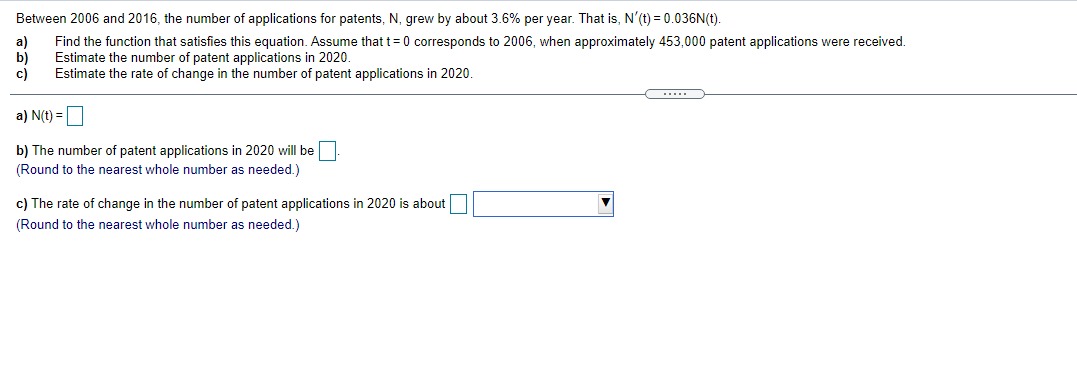
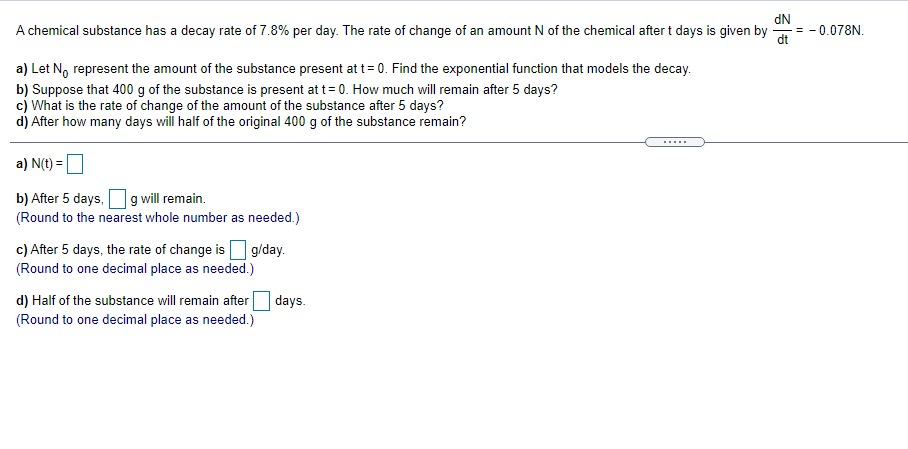
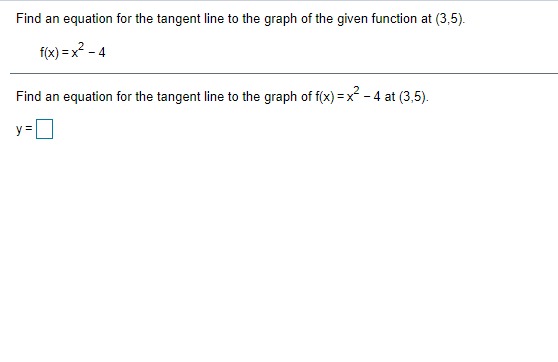
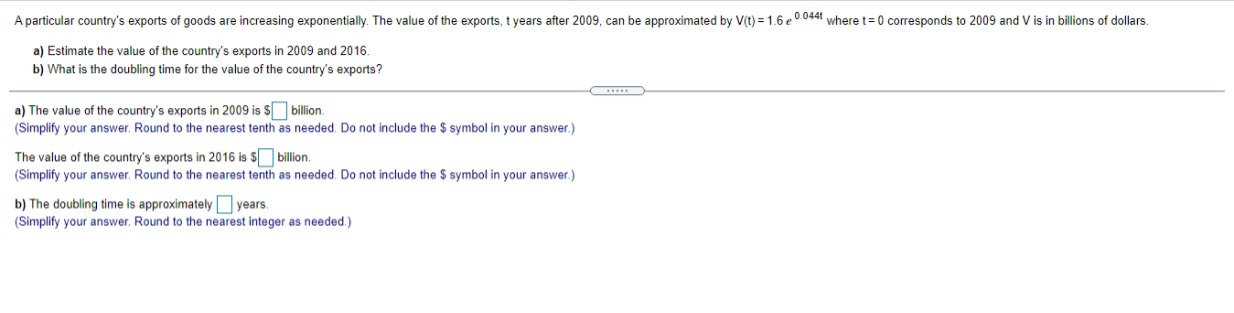
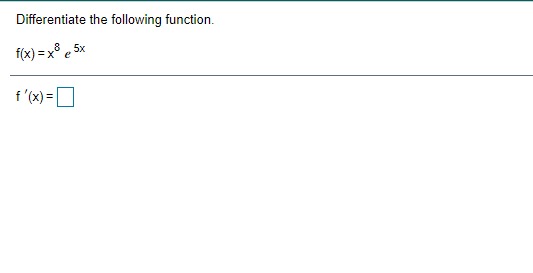
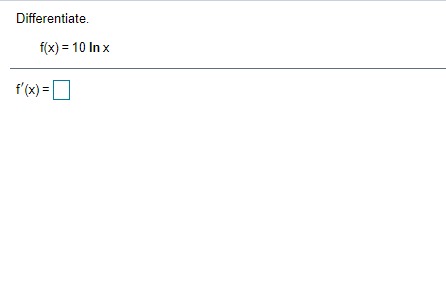
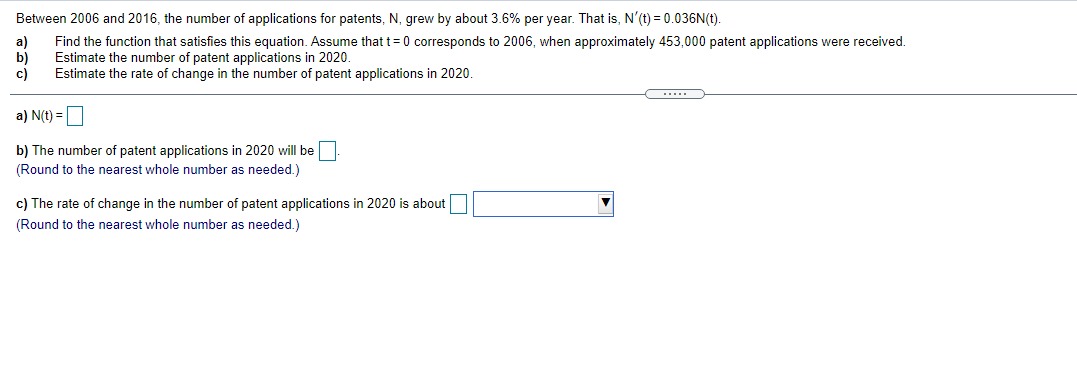
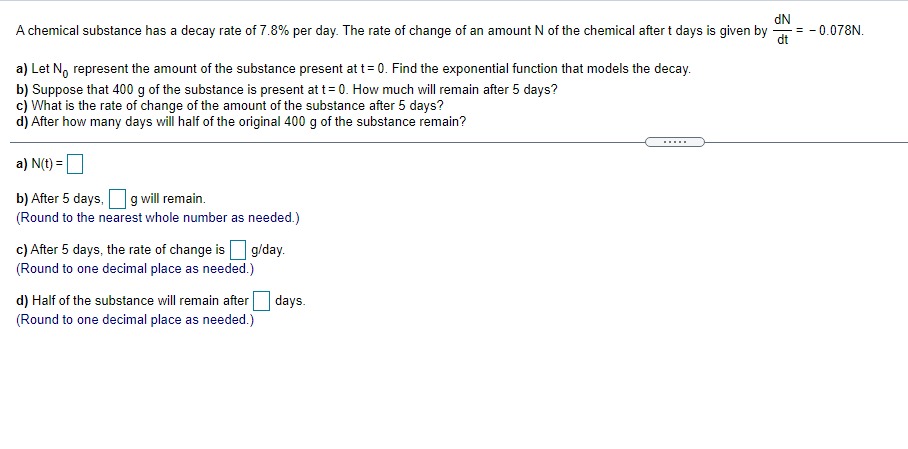
Given In 22 = 3.0910, find the value of the following logarithm without using a calculator. In (22 e ) In (22 e ) = (Type an integer or a decimal.)\fA particular country's exports of goods are increasing exponentially. The value of the exports, t years after 2009, can be approximated by V(t) = 1.6 e :*" where t= 0 corresponds to 2009 and V is in billions of dollars. a) Estimate the value of the country's exports in 2009 and 2016. b) What is the doubling time for the value of the country's exports? a) The value of the country's exports in 2009 is $ billion. (Simplify your answer. Round to the nearest tenth as needed. Do not include the $ symbol in your answer.) The value of the country's exports in 2016 is $ billion. (Simplify your answer. Round to the nearest tenth as needed. Do not include the $ symbol in your answer.) b) The doubling time is approximately years. (Simplify your answer. Round to the nearest integer as needed.)Between 2006 and 2016, the number of applications for patents, N, grew by about 3.6% per year. That is, N'{t} = l].l]36N{t}. it] Find the function that satises this equation. Assume that t= [1 corresponds to 2005, when approximately 453,000 patent applications were received. b) Estimate the number of patent applications in 2021]. {:1 Estimate the rate of change in the number of patent applications in 2020. a] Mo} = b) The number of patent applications in 2020 will be (Round to the nearest whole number as needed.) c] The rate of change in the number of patent applications in 2020 is about "i (Round to the nearest whole number as needed.) ON A chemical substance has a decay rate of 7.8% per day. The rate of change of an amount N of the chemical after t days is given by = - 0.078N. dt a) Let No represent the amount of the substance present at t= 0. Find the exponential function that models the decay. b) Suppose that 400 g of the substance is present at t= 0. How much will remain after 5 days? c) What is the rate of change of the amount of the substance after 5 days? d) After how many days will half of the original 400 g of the substance remain? a) N(t) = b) After 5 days, g will remain. (Round to the nearest whole number as needed.) c) After 5 days, the rate of change is | g/day. (Round to one decimal place as needed.) d) Half of the substance will remain after days. (Round to one decimal place as needed.)Find an equation for the tangent line to the graph of the given function at (3,5). f( x ) = x2 - 4 Find an equation for the tangent line to the graph of f(x) = x -4 at (3,5). V=