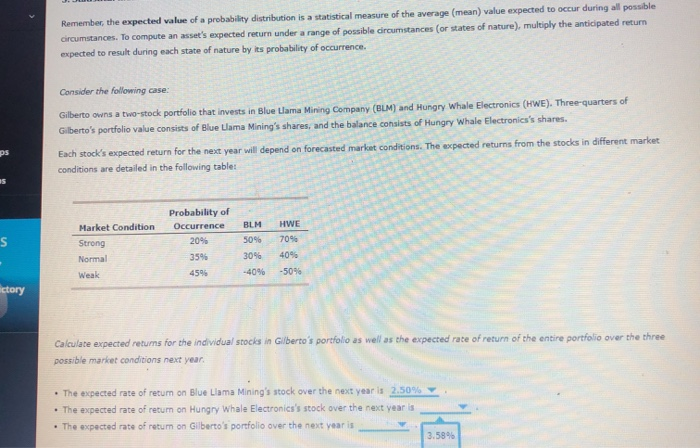
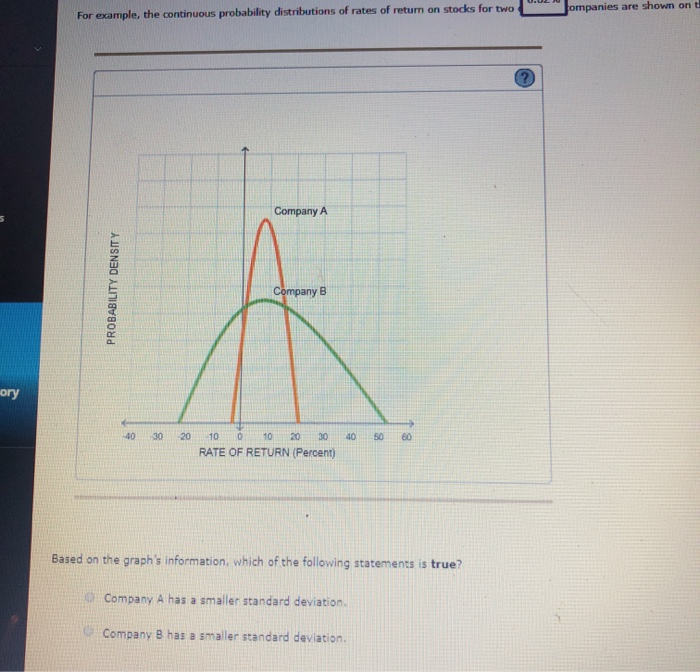
Remember, the expected value of a probability distribution is a statistical measure of the average (mean) value expected to occur during all possible circumstances. To compute an asset's expected return under a range of possible circumstances (or states of nature), multiply the anticipated return expected to result during each state of nature by its probability of occurrence. Consider the following case: Gilberto owns a two-stock portfolio that invests in Blue Llama Mining Company (BLM) and Hungry Whale Electronics (HWE). Three-quarters of Gilberto's portfolio value consists of Blue Ulama Mining's shares, and the balance consists of Hungry Whale Electronics's shares Each stock's expected return for the next year will depend on forecasted market conditions. The expected returns from the stocks in different market conditions are detailed in the following tablet Market Condition Strong BLMHWE Probability of Occurrence 20% 35% Normal 30% Weak ctory Calculare expected returns for the individual stocles in Gilberto's portfolio as well as the expected rate of return of the entire portfolio over the three possible market conditions next year The expected rate of return on Blue Llama Mining's stock over the next year is 2.50 The expected rate of return on Hungry Whale Electronics's stock over the next years The expected rate of retum on Gilberto's portfolio over the next year is 3.58% For example, the continuous probability distributions of rates of return on stocks for two Jompanies are shown on Company A PROBABILITY DENSITY Company B -40 30 20 10 0 10 20 30 RATE OF RETURN (Percent) 40 50 60 Based on the graph's information, which of the following statements is true? Company A has a smaller standard deviation Company B has a smaller standard deviation