requirement:

to do code: (a5.py)

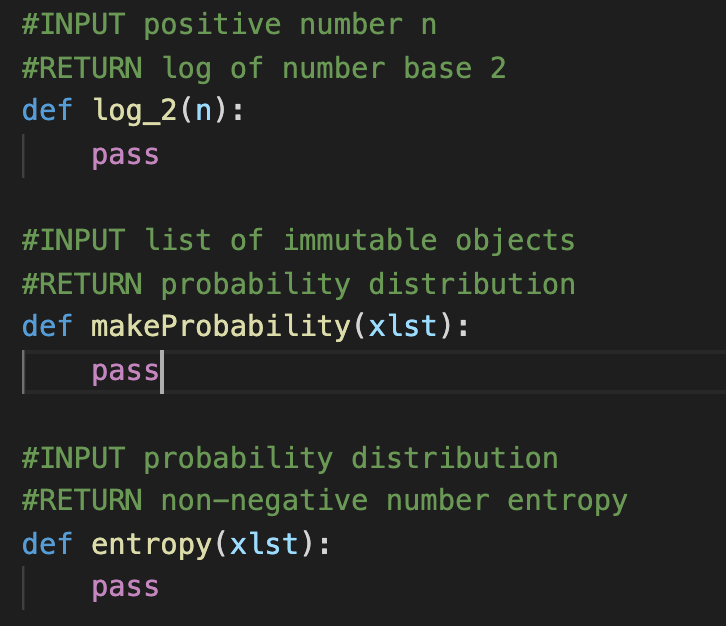
unitest code:

python thanks

In this problem, be calculating what's called Entropy. This is related to the entropy you've seen in physics and chemistry. Entropy is used in Al and ML. Some time ago, Claude Shannon at IBM was working on making a mathematical model of communication. Imagine, you'd have a piece of text, and then his function would give a number indicating how important or significant the message was. What Shannon observed was that importance was really the degree of how surprising the message was. So, in a sense, the message itself wasn't as important as how unexpected it was. He then realized that he could utilize probability as a measure of surprise: Entropy Probability Message not surprising surprising high low For this problem, we are only working with finite probabilities. We can think of probabilities as a list of numbers po, p1, ... , Pn such that Pi > 0, i = 0,1,...,n (1) (2) 1 Po + P1 + P2 + ... + Pn n Pi (3) i=0 Line (3) is usually how it's written using the as a shorthand for addition. We'll learn about this later, but I thought it might be interesting to see it now. Observe it looks a lot like range! You might think about what's similar and what's different. To say in words, they are a finite collection of numbers that are non-negative that sum to exactly one. We can make a list (we'll assume the items are of the same type and immutable) into a probability. Consider x = ["a", "b","a","c","c","a"] 1. gather the items uniquely 2. count each time the item occurs 3. find the total count 4. create a new list of the ratio of count to total For x, we have: 1. {"a": 3, "b":1, "c":2} 2. total count is 6 3. return [3/6,1/6,2/6] (Please note: the fractions here are for understanding but not expecting output like that in your code) We still need to show you how to calculate entropy: (4) entropy entropy(makeProbability(x)) -(Po log2 (Po) + P log2 (P1) + ... + Pn log2 (Pn) 1 6 -(.5(-1.0) + 0.17(-2.58) +.33(-1.58)) 1.46 - log>(3/6) + 1083(1/6) + & 108,(2/6) (5) (6) (7) Because of continuity arguments we treat log2 (0) = 0. Python's math module will correctly state this math error, so you'll have to simply add 0 if the probability is 0. Deliverables Problem 1 Complete log_2 function that returns the log2 of the input Complete makeProbability which takes a list of immutable objects and returns a probability distribution: a list of values [PO, P1, ..., Pn) such that: Pi> 0 for i = 0,1,...,n - Pi = po + p1 + ... + Pr = 1 Complete entropy function #INPUT positive number n #RETURN log of number base 2 def log_2(n): pass #INPUT list of immutable objects #RETURN probability distribution def makeProbability(xlst): pass #INPUT probability distribution #RETURN non-negative number entropy def entropy(xlst): pass class MyTester(unittest. TestCase): def test_Problem1(self): for i,j in zip(xlst, elst): self.assertAlmostEqual(a5.entropy(a5.makeProbability(i)),j,1) S1 = ['a','b', 'a', 'b', 'a', 'b', 'b','b'] s2 = [(1), (2), (3), (4)] s3 = [1] S4 = [1,2] xlst = [s1, s2, 53, 54] elst [0.9544340029249649, 2.0, -0.0, 1.0)