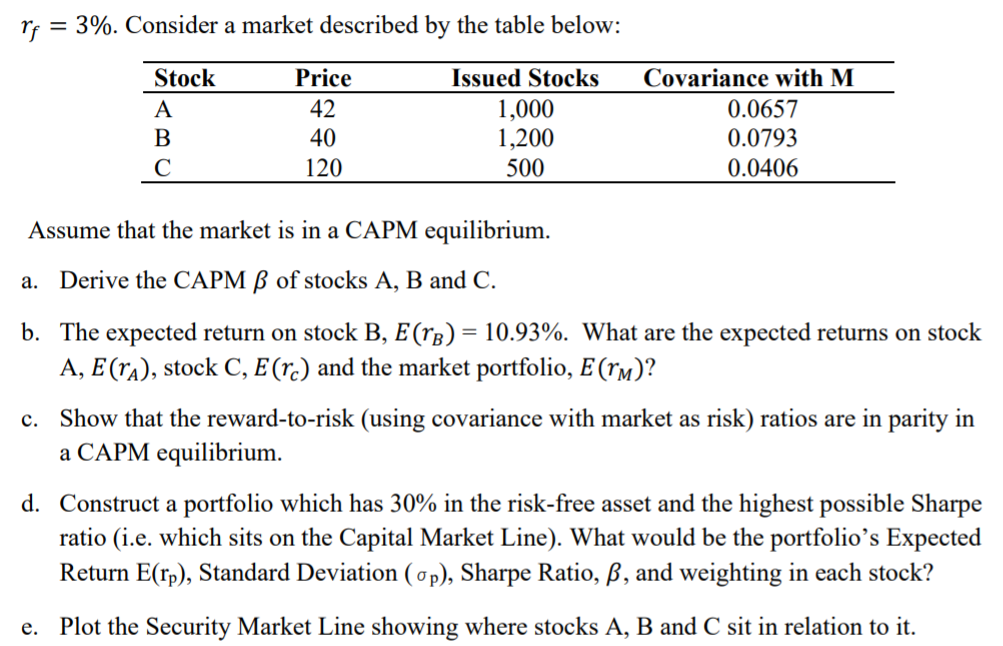
rf = 3%. Consider a market described by the table below: Price 42 Stock A B Issued Stocks 1,000 1,200 500 Covariance with M 0.0657 0.0793 0.0406 40 120 a. Assume that the market is in a CAPM equilibrium. Derive the CAPM of stocks A, B and C. b. The expected return on stock B, E(Tb) = 10.93%. What are the expected returns on stock A, E(ra), stock C, E(rc) and the market portfolio, E(rm)? c. Show that the reward-to-risk (using covariance with market as risk) ratios are in parity in a CAPM equilibrium. d. Construct a portfolio which has 30% in the risk-free asset and the highest possible Sharpe ratio (i.e. which sits on the Capital Market Line). What would be the portfolio's Expected Return E(rp), Standard Deviation (op), Sharpe Ratio, , and weighting in each stock? e. Plot the Security Market Line showing where stocks A, B and C sit in relation to it