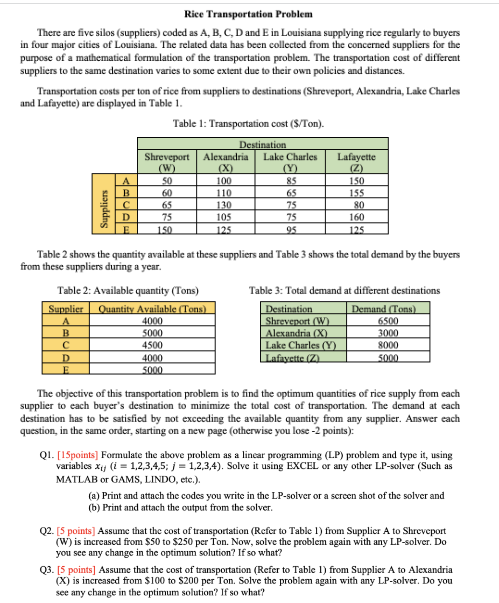
Rice Transportation Problem There are five silos (suppliers) coded as A, B, C, D and E in Louisiana supplying rice regularly to buyers in four major cities of Lowisiana. The related data has been collected from the concerned suppliers for the purpose of a mathematical formulation of the transportation problem. The transportation cost of different suppliers to the same destination varies to some extent due to their own policies and distances. Transportation costs per ton of rice from suppliers to destinations (Shreveport, Alexandria, Lake Charles and Lafayette) are displayed in Table 1. Table 1: Transportation cost (\$/Ton). Table 2 shows the quantity available at these suppliers and Table 3 shows the total demand by the buyers from these suppliers during a year. Table 2: Available quantity (Tons) Table 3: Total demand at different destinations The objective of this transportation problem is to find the optimum quantities of rice supply from each supplier to each buyer's destination to minimize the total cost of transportation. The demand at each destination has to be satisfied by not exceeding the available quantity from any supplier. Answer each question, in the same order, starting on a new page (otherwise you lose 2 points): Q1. [15points] Formulate the above problem as a linear programming (LP) problem and type it, using variables xij(i=1,2,3,4,5;j=1,2,3,4). Solve it using EXCEL or any other LP-solver (Such as MATLAB or GAMS, LINDO, etc.). (a) Print and attach the codes you write in the LP-solver or a screen shot of the solver and (b) Print and attach the output from the solver. Q2. [5 points] Assume that the cost of transportation (Refer to Table 1) from Supplier A to Shreveport (W) is increased from $50 to $250 per Ton. Now, solve the problem again with any LP-solver. Do you see any change in the optimum solution? If so what? Q3. [5 points] Assume that the cost of transportation (Refer to Table 1) from Supplier A to Alexandria (X) is increased from $100 to $200 per Ton. Solve the problem again with any LP-solver. Do you see any change in the optimum solution? If so what