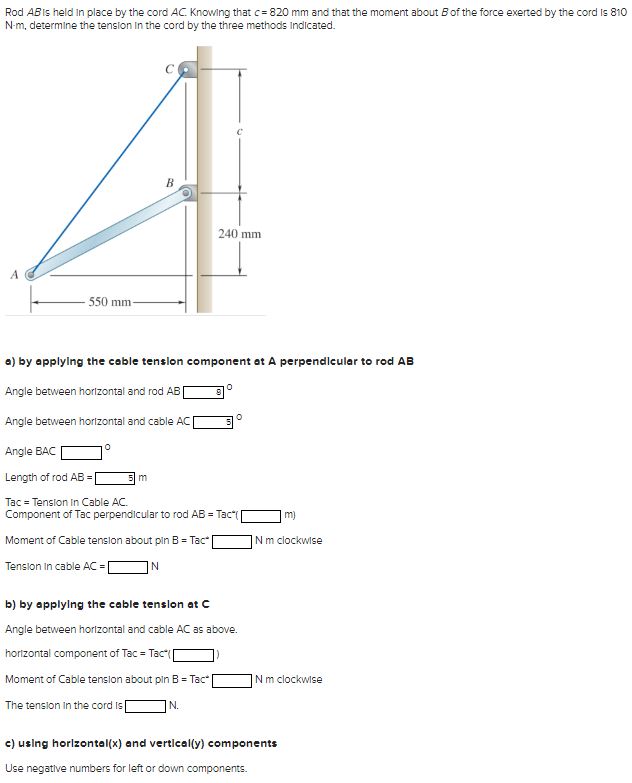
Question: Rod ( A B ) is held in place by the cord ( A C ) . Knowing that (
Rod A B is held in place by the cord A C Knowing that cmathrm~mm and that the moment about B of the force exerted by the cord is mathrmNmathrmm determine the tension in the cord by the three methods indicated.
a by applying the cable tension component at A perpendleular to rod A B
Angle between horizontal and rod A B
Angle between horizontal and cable A C
Angle BAC
Length of operatornamerod A B m
Tac Tension In Cable AC
Component of Tac perpendicular to rod AB Tac
Moment of Cable tenslon about pin mathrmB Tac
N m clockwise
Tension in cable AC N
b by applying the cable tension at C
Angle between horizontal and cable A C as above.
Moment of Cable tension about pin mathrmB Tac
N m clockwise
The tension in the cord is
N
c using horizontal x and vertical y components
Use negative numbers for left or down components.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


