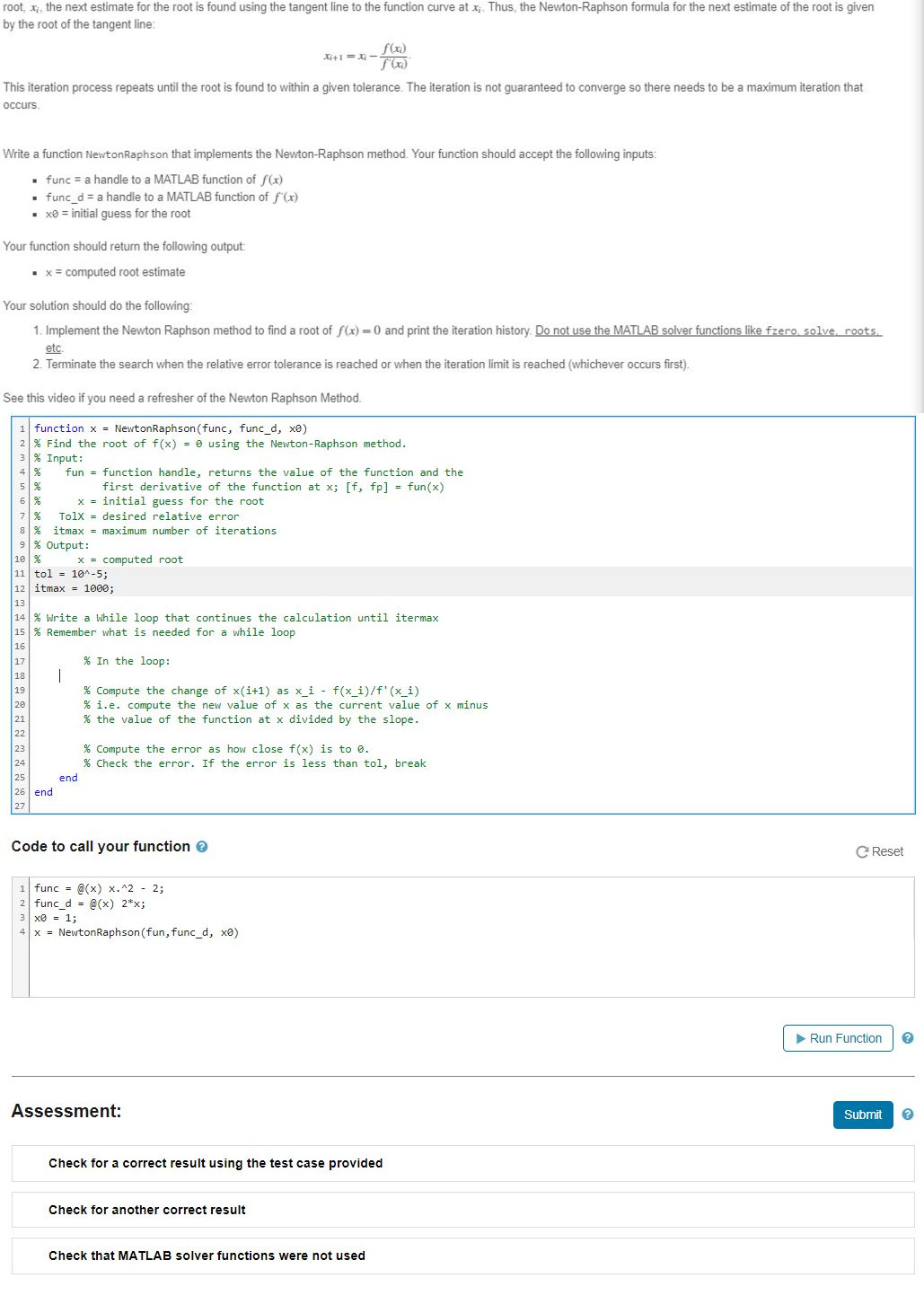
root, $x_i,$ the next estimate for the root is found using the tangent line to the function curve at $x_i.$ Thus, the Newton$-$Raphson formula for the next estimate of the root is given

by the root of the tangent line:

$x_{i+1}=x_i-\frac{f(x_i)}{f^{\text{'}}(x_i)}.$

This iteration process repeats until the root is found to within a given tolerance. The iteration is not guaranteed to converge so there needs to be a maximum iteration that

occurs.

Write a function NewtonRaphson that implements the Newton$-$Raphson method. Your function should accept the following inputs:

func $=$ a handle to a MATLAB function of $f(x)$

func$\_d=$ a handle to a MATLAB function of $f^{\text{'}}(x)$

$x\frac{O}{?}=$ initial guess for the root

Your function should return the following output:

$x=$ computed root estimate

Your solution should do the following:

Implement the Newton Raphson method to find a root of $f(x)=0$ and print the iteration history. Do not use the MATLAB solver functions like fzero, solve. roots.

etc.

Terminate the search when the relative error tolerance is reached or when the iteration limit is reached $($whichever occurs first$).$

See this video if you need a refresher of the Newton Raphson Method.

function $x=$ NewtonRaphson$($func$,$ func$\_$d$,x)$

$\%$ Find the root of $f(x)=0$ using the Newton$-$Raphson method.

$\%$ Input:

fun $=$ function handle, returns the value of the function and the

first derivative of the function at $x$;$[f,fp]=$fun$(x)$

$x=$ initial guess for the root

TolX $=$ desired relative error

itmax $=$ maximum number of iterations

Output:

$\%,x=$ computed root

tol $={10}^{{?}^{{?}^{?}}}-5$;

itmax $=1000$;

$\%$ Write a While loop that continues the calculation until itermax

$\%$ Remember what is needed for a while loop

$\%$ In the loop:

$\%$ Compute the change of $x(i+1)$ as $x_{-}i-f\frac{x_{-}i}{f^{\text{'}}}(x_{-}i)$

$\%$ i$.$e$.$ compute the new value of $x$ as the current value of $x$ minus

$\%$ the value of the function at $x$ divided by the slope.

$\%$ Compute the error as how close $f(x)$ is to $0.$

$\%$ Check the error. If the error is less than tol, break

end

end

Code to call your function $(2)$

Assessment:

Check for a correct result using the test case provided

Check for another correct result

Check that MATLAB solver functions were not used