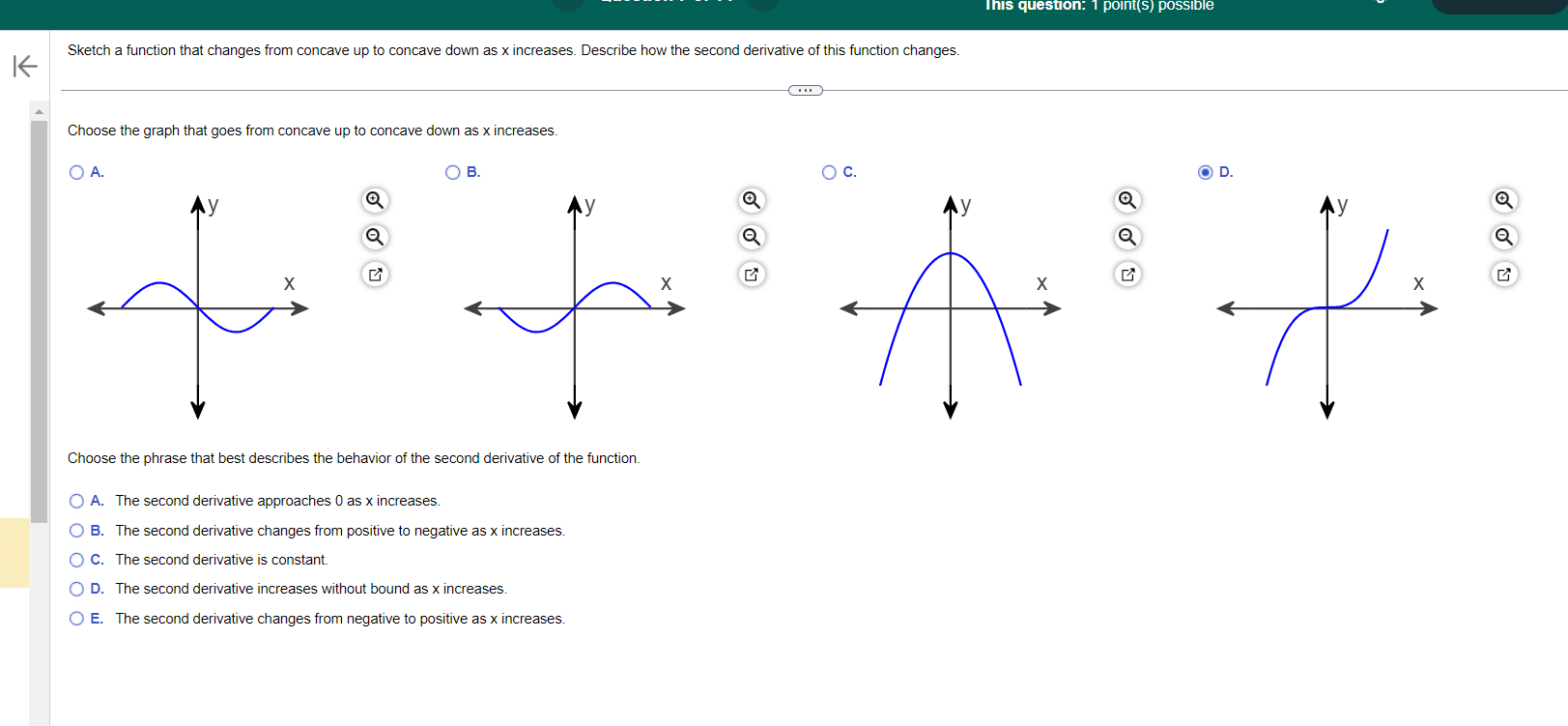
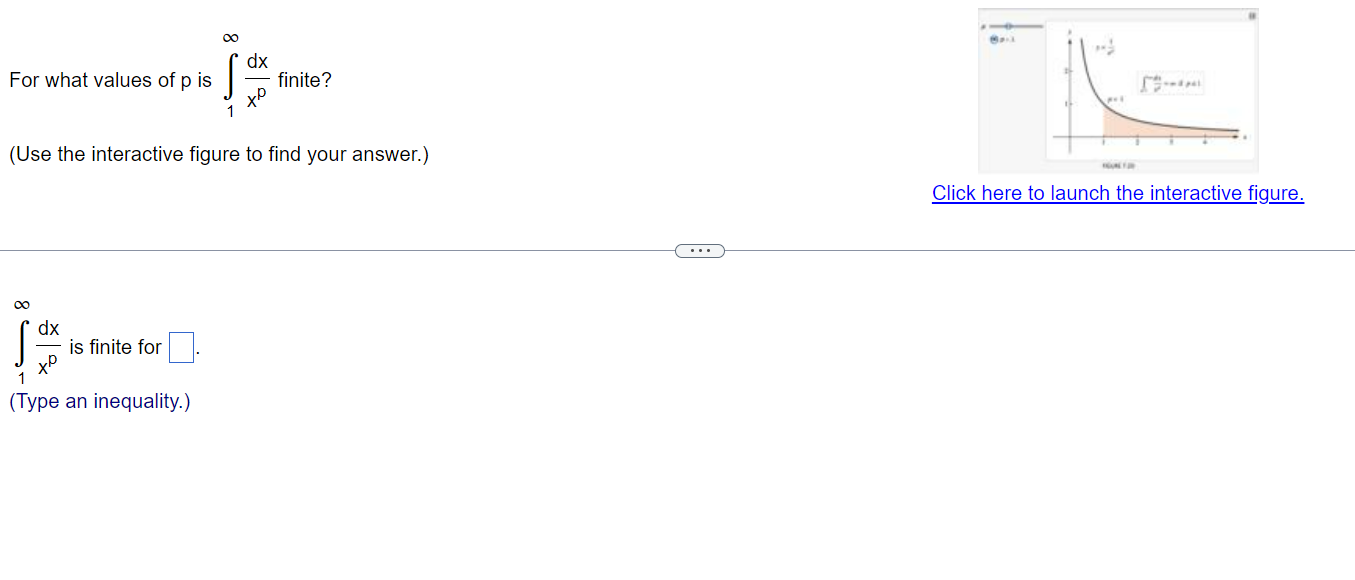
S question: 1 poini(s) possible | Sketch a function that changes from concave up to concave down as x increases. Describe how the second derivative of this function changes. Choose the graph that goes from concave up to concave down as x increases. Q B QO c D. y Q y Q y Q Q 3 2 2 2 X & X |5 X |5 o Choose the phrase that best describes the behavior of the second derivative of the function. . The second derivative approaches 0 as x increases . The second derivative changes from positive to negative as x increases A B. C. The second derivative is constant D. The second derivative increases without bound as x increases. E. The second derivative changes from negative to positive as x increases Explain how, in general, Riemann sum approximations to the area of a region under a curve change as the number of subintervals increases. e Choose the correct answer below. (O A. Ingeneral, as the number of subintervals increases, the Riemann sum approximations to the area of a region under a curve become a more accurate estimate of the actual area of a region under a curve. B. Ingeneral, as the number of subintervals increases, the Riemann sum approximations to the area of a region under a curve become a less accurate estimate of the actual area of a region under a curve. C. No change occurs. o0 dx For what values of p is = finite? 1 X (Use the interactive figure to find your answer.) Click here to launch the interactive figure. 0 dx T is finite for 1 X (Type an inequality.)