Sample code that works for y=sin(ty), y(0)=1:

tFinal = 2*pi;

N = 100;

h=tFinal/N;

t=linspace(0,tFinal,N+1); % type 'help linspace' to see how this works

y=zeros(1,N+1);

yExact=exp(1-cos(t));

y(1) = 1; % setting the initial condition

for n=1:N

y(n+1) = y(n) + h * sin(t(n))*y(n);

end

plot(t,y,t,yExact,'--'); xlabel('t'); ylabel('y'); title('Look, ma! I solved an ODE in MATLAB!');

N = 200;

h=tFinal/N;

t=linspace(0,tFinal,N+1); % type 'help linspace' to see how this works

y=zeros(1,N+1);

yExact=exp(1-cos(t));

y(1) = 1; % setting the initial condition

for n=1:N

y(n+1) = y(n) + h * sin(t(n))*y(n);

end

plot(t,y,t,yExact,'--')

xlabel('t'); ylabel('y'); title('Look, ma! I solved another ODE in MATLAB!');

I'm having trouble modifying the code so that it uses the new equation, keep getting this error:

Invalid expression. When calling a function or indexing a variable, use parentheses. Otherwise, check for mismatched delimiters.

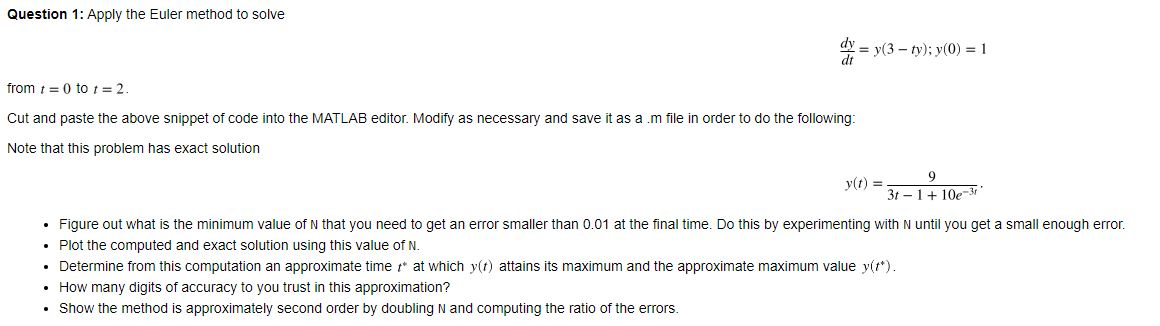
Question 1: Apply the Euler method to solve y = y(3 - ty); y(0) = 1 from t = 0 to 1 = 2. Cut and paste the above snippet of code into the MATLAB editor. Modify as necessary and save it as a .m file in order to do the following: Note that this problem has exact solution y(t) = 3-1 + 10e-31 Figure out what is the minimum value of N that you need to get an error smaller than 0.01 at the final time. Do this by experimenting with N until you get a small enough error. Plot the computed and exact solution using this value of N. Determine from this computation an approximate time at which y(t) attains its maximum and the approximate maximum value y(t*). How many digits of accuracy to you trust in this approximation? Show the method is approximately second order by doubling N and computing the ratio of the errors