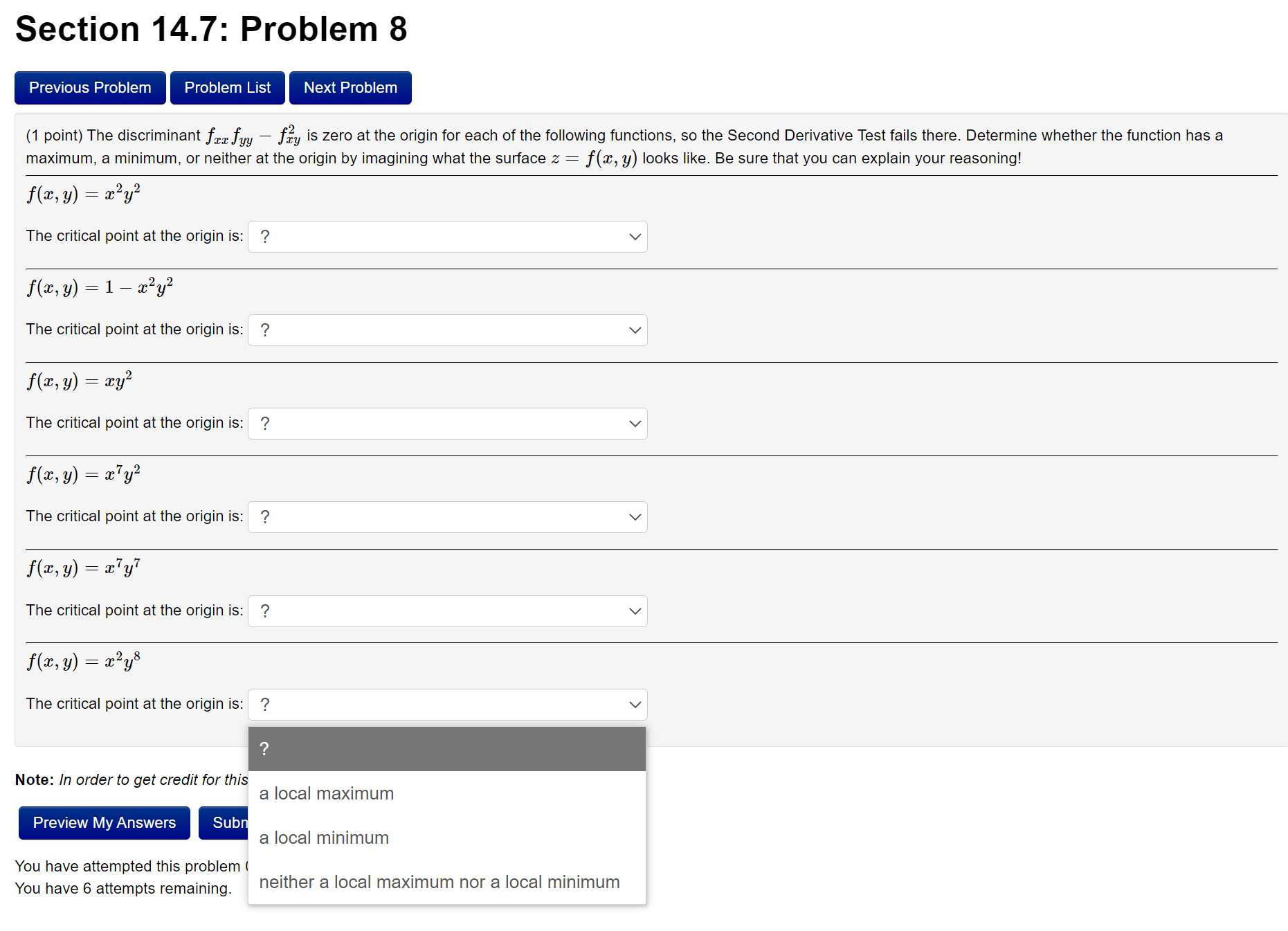
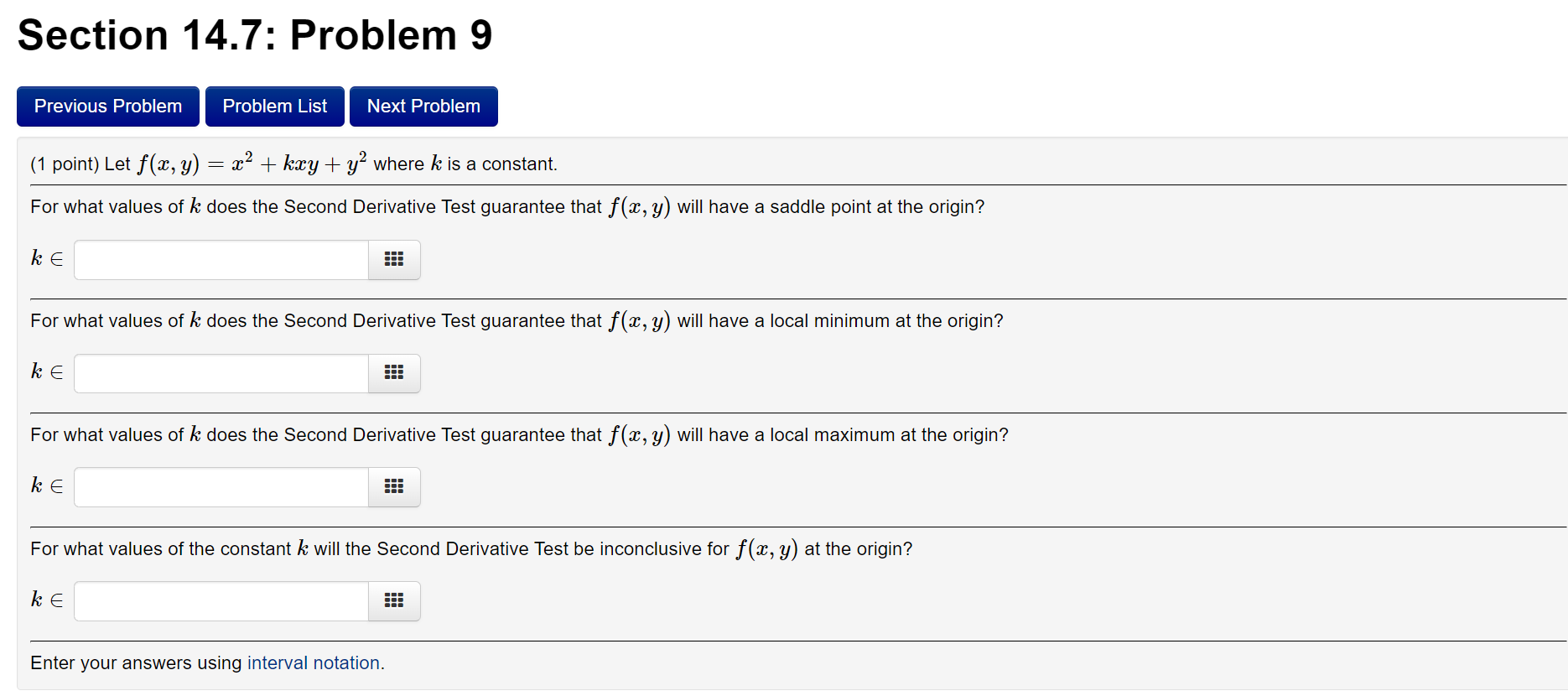
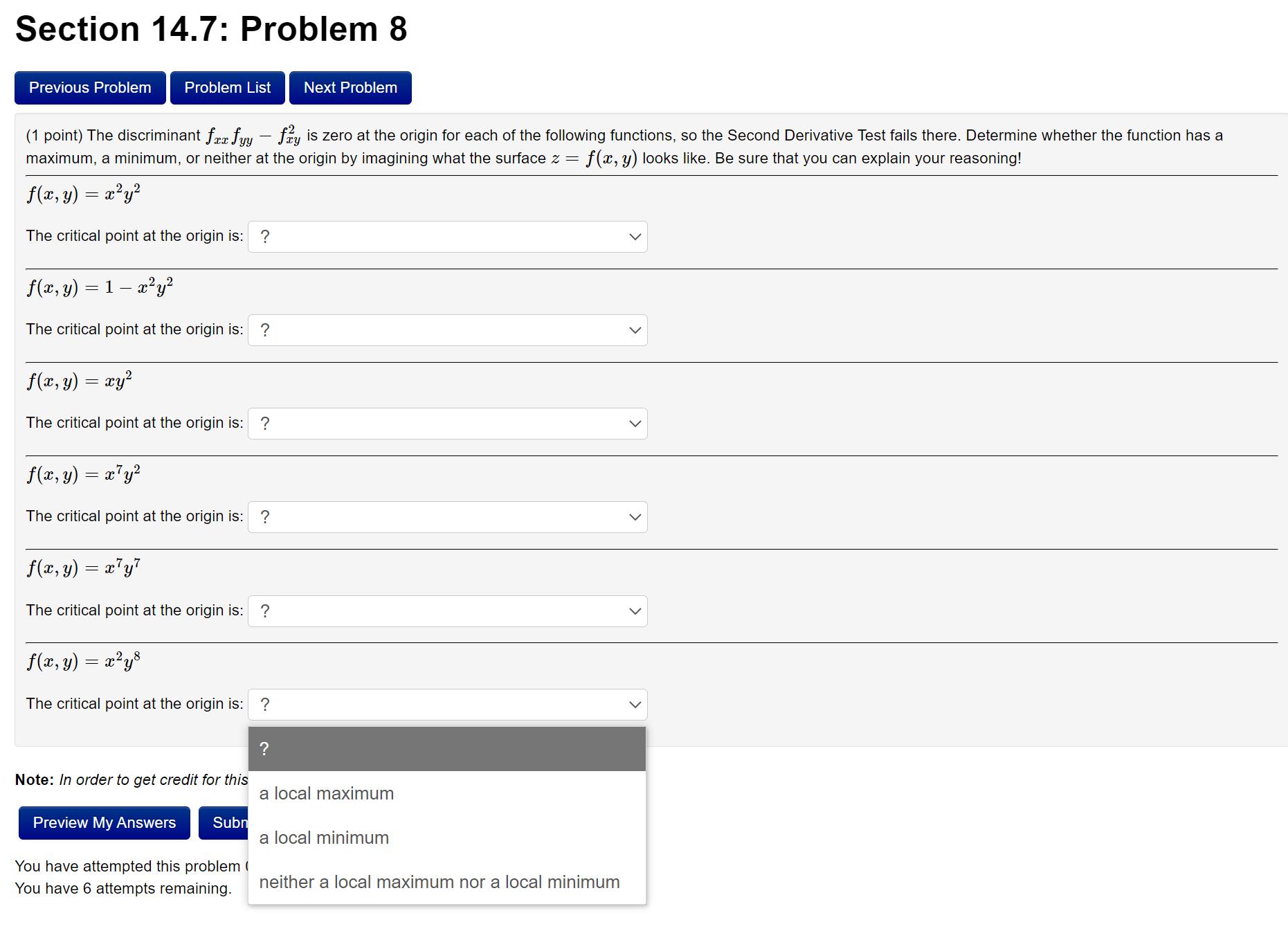
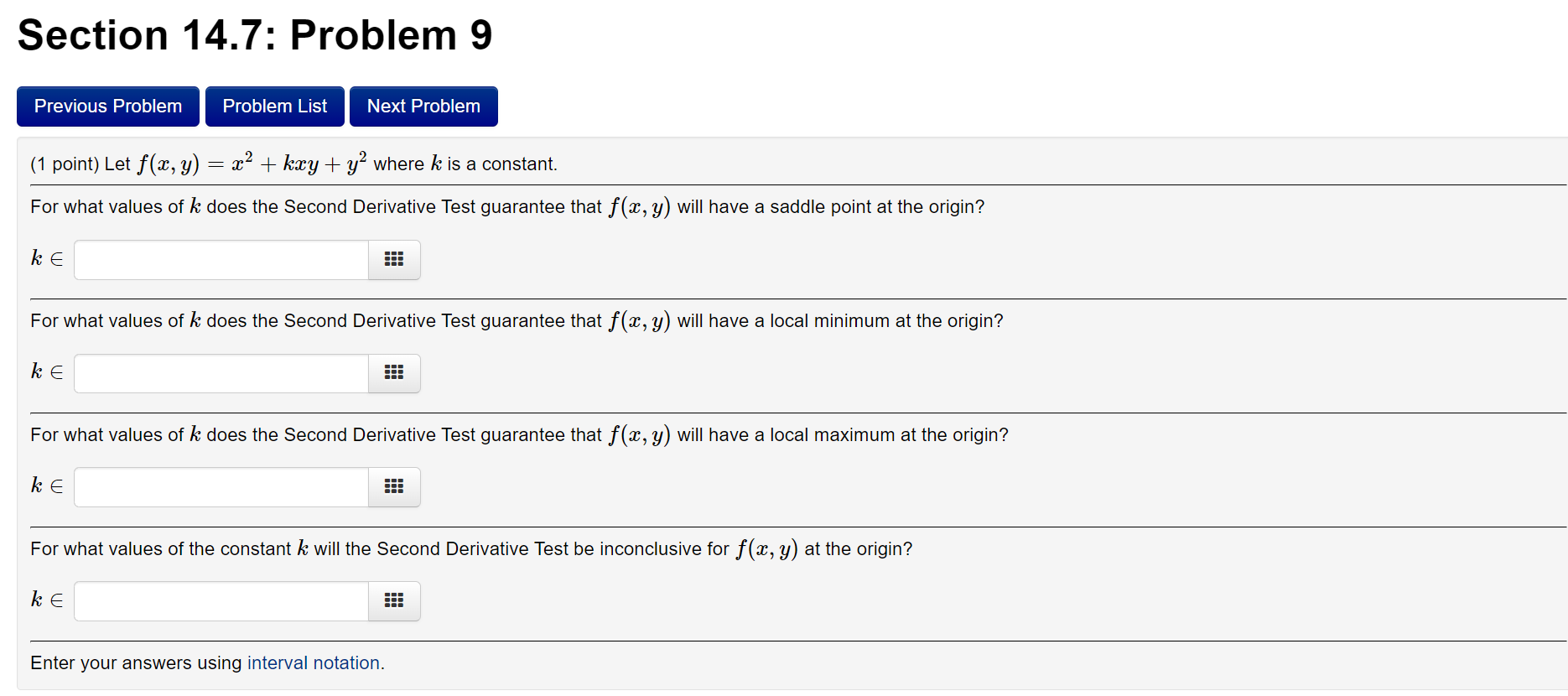
Section 14.7: Problem 8 (1 point) The discriminant J",;,,j'W y is zero at the origin for each of the following functions, so the Second Derivative Test fails there. Determine whether the function has a maximum, a minimum, or neither at the origin by imagining what the surface 2. : f(:t, 3,!) looks like. Be sure that you can explain your reasoning! f(=v, y) = $2y2 The critical point at the origin is: ? v ns, 1;) = 1 , $2312 The critical point at the origin is: ? v 2 f(% y) : $3; The critical point at the origin is: ? v Km 3;) : 3W2 The critical point at the origin is: '? v fur. y) : $7y7 The critical point at the origin is: ? v f(w, y) : $2y8 The critical point at the origin is: '? v Note: In order to get credit for this . a local maXImum Preview MyAnswers Sub . . a local minimum You have attempted this problem 1 You have 6 attempts remaining neither a local maXImum nor a local minimum Section 14.7: Problem 9 (1 point) Let f(:r:, y) : 1:2 + kmy + y2 where k is a constant. For what values of k: does the Second Derivative Test guarantee that f(.1:, y) will have a saddle point at the origin? k 6 EEE For what values of 1:: does the Second Derivative Test guarantee that f(.1:, y) will have a local minimum at the origin? k 6 EEE For what values of k: does the Second Derivative Test guarantee that f(:t, y) will have a local maximum at the origin? k6 For what values of the constant k will the Second Derivative Test be inconclusive for f(:c, y) at the origin? k6 Enter your answers using interval notation