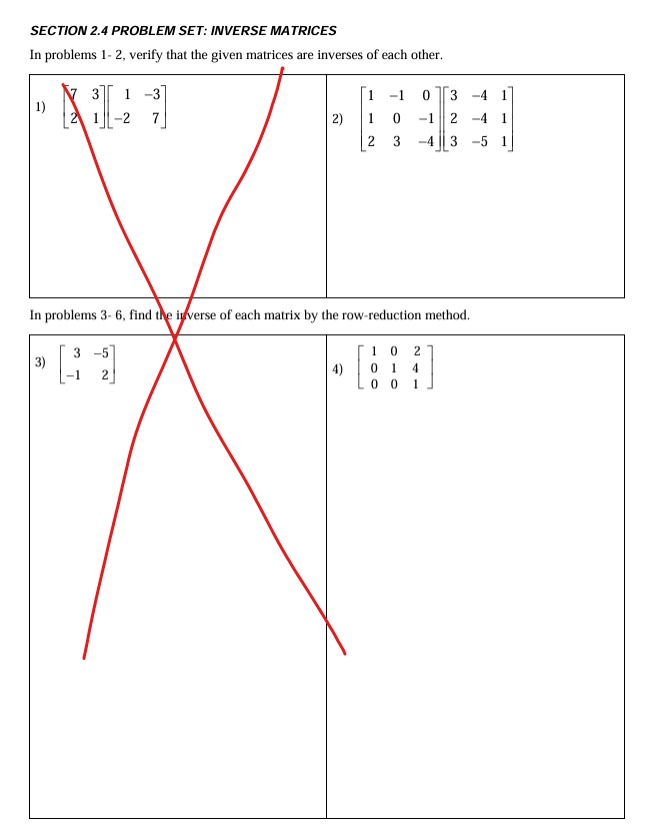
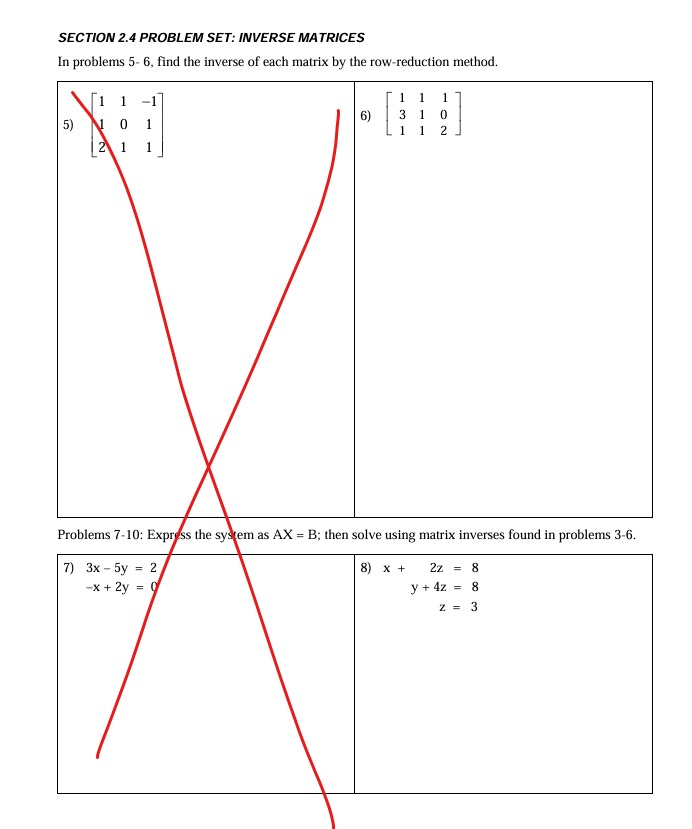
SECTION 2.4 PROBLEM SET: INVERSE MATRICES In problems 1- 2, verify that the given matrices are inverses of each other. -1 0 3 -4 2) 0 2 -4 2 3 13 -5 In problems 3- 6, find the isverse of each matrix by the row-reduction method. 1 0 2 4) 0SECTION 2.4 PROBLEM SET: INVERSE MATRICES In problems 5- 6, find the inverse of each matrix by the row-reduction method. 6) 3 5) 0 N 2 1 Problems 7-10: Express the system as AX = B; then solve using matrix inverses found in problems 3-6. 7) 3x - 5y = 2 8) x + 2z = 8 -x + 2y = Q y + 42 = 8 Z = 3SECTION 2.4 PROBLEM SET: INVERSE MATRICES Problems 9-10: Express the system as AX = B; then solve using matrix inverses found in problems 3-6. 9) x+ y - z = 2 10) x + y + z = 2 X + Z = 7 3x + y = 7 x+ y + z = 13 x + y + 2z = 3 1 1) Why is it necessary that a matrix be a square 12) Suppose we are solving a system AX = B by matrix for its inverse to exist? Explain by the matrix inverse method, but discover A relating the matrix to a system of equations. has no inverse. How else can we solve this system? What can be said about the solutions of this system