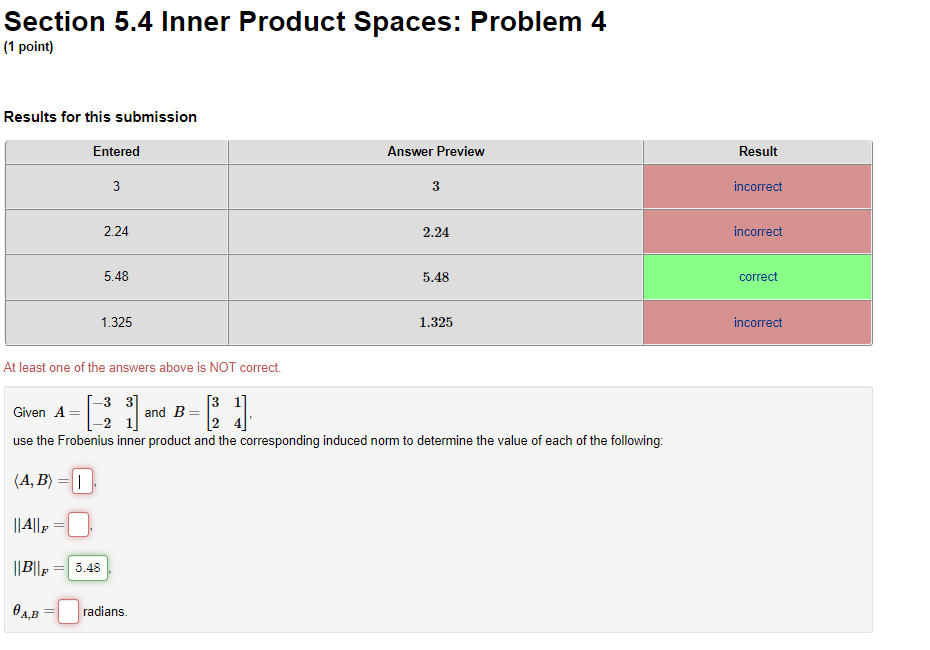
Section 5.4 Inner Product Spaces: Problem 3 (1 point) Use the inner product = / f(x)g(x)dx in the vector space C"[0, 1] to find , IIfll. |Igl|, and the angle Of., between f(x) and g(I) for f(x) = -10x2 - 9 and g(x) = 9r + 1. (f,g) =1 = Ilgll = Of.g radians.Section 5.4 Inner Product Spaces: Problem 4 (1 point) Results for this submission At least one of the answers above is NOT correct. Given A: [3 3] and B: [3 1], 1 2 4 use the Frobenius inner product and the corresponding induced norm to detennine the value of each of the following: Section 5.4 Inner Product Spaces: Problem 5 (1 point) Results for this submission Entered Answer Preview Result 1564 1564 correct 30.87 30.87 correct 54.15 54.15 correct 0.360771808853443 cos (0.935624656581183) incorrect At least one of the answers above is NOT correct. If p(x) and q() are arbitrary polynomials of degree at most 2, then the mapping

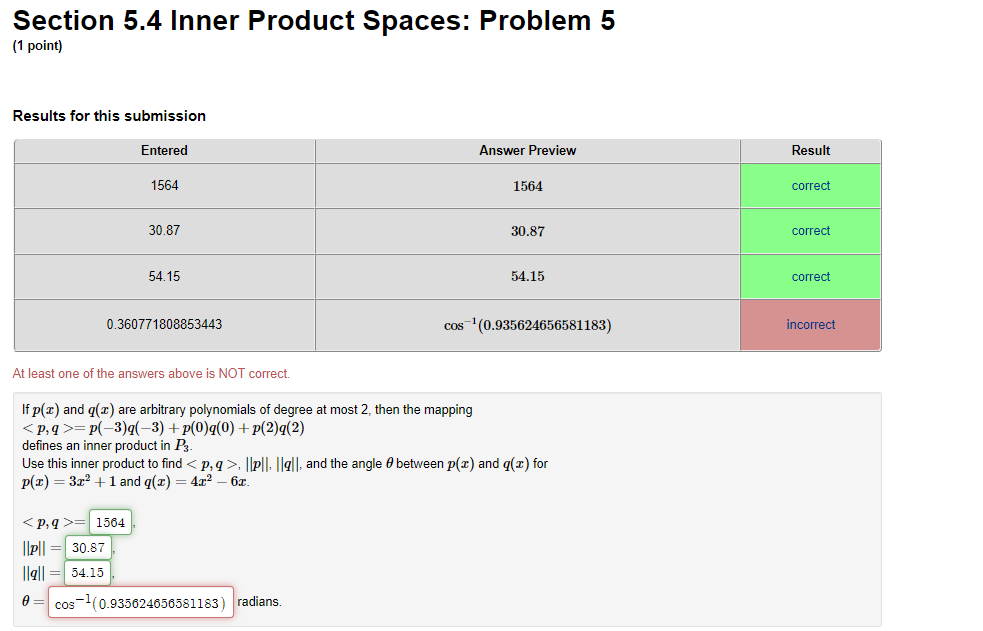
=p(-3)q(-3) + p(0)q(0) + p(2)q(2) defines an inner product in P3. Use this inner product to find , Ilpll, ||gl|, and the angle @ between p(x) and q(I) for p(x) = 3x2 + 1 and q(x) = 4x2 - 61.

= 1564 Ilpll = 30.87 llall = 54.15 cos ( 0.935624656581183 ) radians.Section 5.4 Inner Product Spaces: Problem 6 (1 point) Use the inner product

=p(-1)q(-1) + p(0)q(0) + p(3)q(3) in Pa to find the orthogonal projection of p(x) = 3x2 + 6x + 7 onto the line L spanned by q(r) = 4x2 - 5x - 1. projL(P) =